2015-10-22
395
Пусть имеется неделимых производственных единиц, которые в дальнейшем мы для краткости будем называть центрами; каждую из этих производственных единиц требуется расположить в одном из 
возможных мест. Затраты, связанные непосредственно с помещением центра 
на место 
("затраты на установку"), равны 
. Известны "расстояния" 
от места до места (числа вовсе не обязаны равняться соответствующим геометрическим расстояниям; они являются лишь оценкой затрат, связанных с перемещением из в ). Заданы, кроме того, производственные "потоки" 
из центра в центр .
Отметим, что, не умаляя общности, можно положить 
. Действительно, в случае 
введем дополнительные фиктивные центры 
, положив для них 
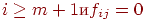при 
при 
или 
.
Нашей целью является назначение (закрепление) центров по местам, минимизирующее суммарные затраты. Каждое такое назначение представляет собой перестановку 
чисел 
; при этом любое из проводимых закреплений центра за местом 
описывается соответствием 
. Для любого назначения мы имеем, во-первых, затраты на взаимосвязь между парами центров; мы будем предполагать, что эти затраты при помещении центра в место и центра в место 
равны произведению величины потока между и на расстояние между и , проходимое этим потоком, то есть составляют 
. Таким образом, требуется найти перестановку 
чисел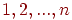 
, минимизирующую суммарные затраты
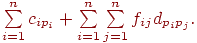
| (7.23) |
Иногда в подобных задачах накладывается следующее дополнительное требование: каждый центр может быть помещен не в любое место, а лишь в одно из мест из данного списка 
, скажем, по соображениям веса, габаритов и тому подобное. Тогда следует присоединить к задаче условие
| (7.24) |
В случае независимости производственных центров все 
, и задача минимизации (7.23.) по всем перестановкам превращается в задачу о назначениях. В этом случае 
можно интерпретировать как своеобразную "меру нежелательности" назначения 
или, попросту говоря, как убытки, связанные с таким назначением. Наоборот, в других задачах можно пренебречь затратами на установку 
или считать все эти затраты одинаковыми, так что речь идет только о минимизации суммарных "затрат по взаимодействию", то есть второго слагаемого в (7.23.).
Модель (7.23.)-(7.24.) имеет весьма широкие практические приложения, отражая существенные черты многих современных задач проектирования. Так, она может быть использована в вопросах планирования расстановки оборудования в целях машиностроительных или химических предприятий. С другой стороны, она же может найти применение для задач о проектировании расположения деталей в ячейках вычислительных и управляющих устройств (например, при нахождении схем монтажа платы, минимизирующих суммарную длину соединений). Здесь эта модель описана в нарочито общих терминах в надежде, что различные более конкретные интерпретации читатель этой лекции найдет сам.
