Розрахункова робота №9
| Номер варіанту | Завдання 1 | Завдання2 | Завдання 3 |
| №1а | №5б | №3б | |
| №1б | №5в | №3в | |
| №1в | №5г | №4а | |
| №1г | №6а | №4б | |
| №2а | №6б | №4в | |
| №2б | №6в | №4г | |
| №2в | №6г | №4д | |
| №2г | №6д | №5а | |
| №3а | №1а | №5б | |
| №3б | №1б | №5в | |
| №3в | №1в | №5г | |
| №4а | №1г | №6а | |
| №4б | №2а | №6б | |
| №4в | №2б | №6в | |
| №4г | №2в | №6г | |
| №4д | №2г | №6д | |
| №5а | №3а | №1а | |
| №5б | №3б | №1б | |
| №5в | №3в | №1в | |
| №5г | №4а | №1г | |
| №6а | №4б | №2а | |
| №6б | №4в | №2б | |
| №6в | №4г | №2в | |
| №6г | №4д | №2г | |
| №6д | №5а | №3а | |
| №6е | №5б | №3б | |
| №1а | №5в | №3в | |
| №1б | №5г | №4а | |
| №1в | №6а | №4б | |
| №1г | №6б | №4в |
Задача 1. Нехай задані квантори: P(x) = “x – просте число”, Q(x)= “x – раціональне число, I(x)= “x – ірраціональне число, H(x)= “x – парне число, R(x,y)= “x ділиться на y”.
Прочитайте подані висловлення та знайдіть їх істинні сні значення:
а) (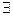 x) (
x) (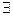 y)[I(x)
y)[I(x) 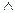 I(y)n
I(y)n 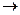 Q(x-y)];
Q(x-y)];
б) (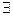 x)[]P(x)
x)[]P(x) 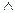 R(x, -2)];
R(x, -2)];
в)(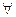 x) [(x
x) [(x 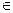 Z)
Z) 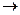 R(x,x)];
R(x,x)];
г)(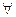 x)(
x)(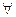 y)[P(x)
y)[P(x) 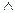 P(y)
P(y) 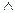 R(x,y)
R(x,y) 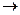 x=y].
x=y].
Задача 2.Запишіть і знайдіть істинні сні значення заперечення висловлень з попередньої задачі.
Задача 3.Запишіть заперечення таких предикатів:
а)(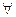 x)[x
x)[x 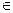 C)
C) 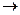 (x>0)
(x>0) 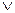 (x<0)
(x<0) 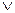 (x=0)];
(x=0)];
б))(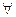 x)[x
x)[x 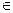 Q)
Q) 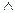 (x2=2)];
(x2=2)];
в) (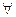 x)(
x)(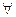 y)[(x
y)[(x 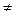 0)
0) 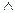 (y
(y 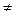 0)
0) 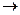 (xy
(xy 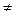 0)].
0)].
Задача 4.Знайдіть істинні сні значення і заперечення поданих висловлень, записавши їх попередньо в символічній формі:
а)існують такі цілі числа, що не діляться самі на себе;
б)існує ціле число, на яке не ділиться жодне ціле число;
в) існує ціле число, на яке не ділиться жодне інше ціле число;
г) існує найменше ціле число, яке ділиться на задані цілі числа a іb;
д) довільне дійсне число є коренем деякого многочлена з цілими коефіцієнтами.
Задача 5. З’ясуйте, чи будуть наведені пари висловлень запереченням одне одного:
а)деякі прості числа парні. Існують непарні прості числа;
б)існують многочлени, що мають недійсні корені. Усі многочлени мають дійсні корені;
в) деякі цілі числа діляться на 0. Довільне ціле число не ділиться на 0;
г)сума деяких двох многочленів степеня n є многочленом степеня n. Сума двох многочленів степеня n є многочленом степеня n.
Задача 6.Прочитайте і запишіть словами прочитане та визначте істинні сні значення висловлень Mx=My= R:
а)(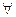 x)[(x2-1)=(x-1) (x+1)];
x)[(x2-1)=(x-1) (x+1)];
б)(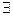 x)[|x|
x)[|x| 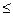 0];
0];
в)(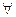 x)[|x|>0];
x)[|x|>0];
г)(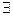 y)[5+y=5];
y)[5+y=5];
д) (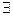 y)[y2+y+1=0];
y)[y2+y+1=0];
е)(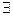 x)[x3<x2]/
x)[x3<x2]/
Задача 7.Запишіть наступні речення використовуючи символи кванторів:
а) “Існує число х таке що х+10=2;
б)у крайньому випадку хоча б одне число у є коренем рівняння ау2+ву+с=0;
в)яке б не було число z, z+0=z;
г) рівняння f(x)=0має хоча б один корінь;
д)будь-яке число або додатне, або від’ємне або рівне нулю.
 2015-10-22
2015-10-22 343
343







