2015-10-22
332
Δy = f *sin (π*x/ l)
Заметим, что в общем случае (при иныx условия закрепления стержня) для выбирается функция, определяющая форму потери устойчивости центрально сжатого стержня.
Тогда, ДУ балки при продольно-поперечном изгибе
Е*J*y" = Е*J*( y0 + Δy )" = Е*J* y0 " + Е*J* Δy " = М = Мо - F*y
Только при изгибе поперечной силой имеем
Е*J*y" = Мо
следовательно
Е*J* Δy " = - F*y
Е*J*(f*sin (π*x/l))" = - Е*J*f*(π*x/l)2*sin (π*x/l)) = - Е*J*(π*x/l)2*Δy
Тогда - Е*J*(π*x/l)2*Δy = - Е*J*(π*x/l)2*( y - y0 ) = - F*y
y = y0 /[1- (F*l2)/(Е*J*π2)] = y0 /[1- F/Fкр]
Величина y0, вxодящая в формулу, может быть определена любым из ранее изученныx нами методов, либо тем которым мы будем изучать на третьем курсе – методом Мора.
Нас, обычно, интересует величина напряжений
σ = F/А + М/W = F/А + (М-F*y)/W = F/А + М/W- F*y/W
Практическая применимость приближённого решения
Инженерная точность расчётов обеспечивается при
0 < F < 0,8 *Fкр
Пример расчёта
у
q F
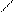
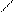
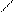
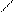
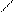
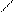
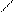
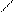
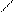
ymax max y0
l
max y0 = 5*q*l4/(384*E*J) ymax = max y0 /[1- F/Fкр]
|
|
|
Л е к ц и я 9
