Метод максимума правдоподобия

Постановка задачи оценивания при использовании мето­да максимума правдоподобия в основном совпадает с постановкой задачи при использовании метода наименьших квадратов.

Пусть необходимо оценить некоторый n-мерный вектор неиз­вестных параметров а, в качестве которых можно рассматривать, например, вектор параметров орбиты ИСЗ. Относительно этого вектора известно лишь то, что он принадлежит допустимому мно­жеству . Измерения , l×l, i =0,1, 2,..., N связаны с неиз­вестными параметрами таким образом, что удается построить плотность вероятностей p(y^N/a), где y^N попрежнему обозначает блочный вектор . Функцией правдоподобия вектора а называют неотрицательную вещественную функцию L(y^N/a), пропорциональную плотности распределения p(y^N/a) [11], т. е.

где множитель может зависеть от ,но не зависит от а. При этом функция правдоподобия рассматривается как функция а при фиксированных значениях y^N, соответствующих проведенным измерениям.

Оценкой максимального правдоподобия для заданной функции правдоподобия L(y^N/a) является вектор , удовлетворяющий со­отношению

В общем случае не требуется, чтобы функция правдоподобия L(y^N/a) была дифференцируема по а; при этом оценка макси­мального правдоподобия не обязательно единственна [11].

После этих общих сведений об оценке максимального правдопо­добия перейдем к конкретным ситуациям, в которых удается по­строить функцию L(y^N/a).

Пусть модель измерений имеет вид

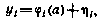
причем плотность вероятностей ошибки измерений р( ) известна при всех i. Тогда для всей обрабатываемой выборки можем запи­сать

где — вектор-функция вида ; — блочный вектор вида .

Из (3.177) следует, что . Положив k=1, получим, что . Таким образом, для построе­ния функции*правдоподобия необходимо знать плотность вероятностей ошибок измерения . От вида этого закона зависит структу­ра соответствующего алгоритма оценивания. Оценки максималь­ного правдоподобия, как уже указывалось, находятся из условия (3.177). Необходимое условие экстремума функции правдоподобия

записывается в виде . Это условие следует рассматривать как систему из п нелинейных алгебраических уравнений, среди корней которой находятся оценки максимального правдоподобия, которые должны также удовлетворять достаточному условию (3.176). В математической статистике доказывается, что, в частно­сти, при нормальном законе распределения ошибок р( ) оценка максимального правдоподобия является состоятельной [14]. Поэто­му случай нормального распределения вектора представляет са­мостоятельный интерес.