Рекуррентная форма метода наименьших квадратов

Установим связь между рассмотренными выше рекур­рентными байесовскими алгоритмами и алгоритмом метода наи­меньших квадратов. С этой целью рассмотрим следующую ситуа­цию. Пусть имеется выборка из k векторов измерений 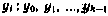, до момента включительно, связанных с оцениваемым век­тором параметров соотношением

Тогда, вводя обозначения Н, аналогично (3.134), (3.142) и (3.145), получим для рассматриваемой выборки

Пусть теперь в момент реализован еще один вектор измерений

Введем блочные векторы

В соответствии с процедурой метода наименьших квадратов и вве­денными обозначениями 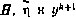имеем для выборки объемом k+1 векторов выражение для оценки вектора , записанное по аналогии с (3.144):

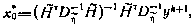
где , здесь - весовая матрица выборки

— весовая матрица, соответствующая вектору .

Корреляционная матрица ошибок оценок вектора х₀

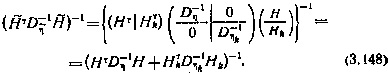
Введем обозначения:

—корреляционная матрица, соответствующая

выборке у^k+1;

— корреляционная матрица, соответствующая

выборке y^k+1.

Тогда с учетом (3.148) и введенных обозначений будем иметь

Это выражение тождественно соответствующему выражению ли­нейного фильтра Калмана (3.41) с той лишь разницей, что в (3.149) в отличие от фильтра Калмана фигурирует матрица , а не прогнозированная матрица . Это естественно, поскольку в постановке задачи оценивания по методу наименьших квадратов оцениваем вектор параметров, в данном случае вектор начальных условий , а не текущий вектор состояния линейной динамической системы . Метод наименьших квадратов можно использовать и для получения оценки текущего состояния линейной динамической системы. Пусть требуется оценить состояние ли­нейной динамической системы с фундаментальной матрицей где i и i -1 - моменты времени, в которые определены векторы состояния соответственно: .

Поставим задачу оценить состояние x_h в момент с номером k по измерениям до момента k —1 включительно.

Тогда для моментов с номерами i и k можно записать , для выборки объемом k имеем

Или

Где

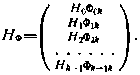
Для выборки объемом k получим

Так как состояние х_к оценивается по измерениям до момента k —1 включительно, то — корреляционная матрица ошибок прогнози­рованной оценки , определяемой идентично соответствующей оценке фильтра Калмана.

Если теперь добавить к выборке y^k вектор y_k, определяемый по формуле

то с учетом (3.149) выражение для корреляционной матрицы оши­бок оценки состояния x_k по выборке y^k+1 примет вид

т. е. тождественно выражению (3.41), определяющему корреляци­онную матрицу ошибок оценки, получаемой с помощью фильтра Калмана. Используя матричное тождество (3.39), можно записать (3.152) в виде

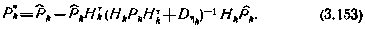
Выражение для оценки x_k по методу наименьших квадратов в соответствии с (3.144) и введенными обозначениями для имеет вид

где

Подставим вместо его выражение (3.153) и учтем структуру блочных матриц и вектора y^k+1:

где - прогнозированная оценка состояния x_h по

измерениям

Выражения (3.153), (3.154), (3.156) эквивалентны соответст­вующим выражениям линейного фильтра Калмана.