В настоящее время метод наименьших квадратов находит самое широкое применение при построении оценок параметров движения летательных аппаратов и, в первую очередь, при определении орбит космических аппаратов. Поэтому в данном разделе вначале излагается общая (классическая) идея метода наименьших квадратов [6, 29], а затем приводится его изложение применительно к задаче определения оценок состояния космических аппаратов [17].
Введем модель измерений в виде:

где уi — l -мерный вектор измерений, реализуемых в момент ti, 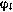 — нелинейная вектор-функция, связывающая вектор измеряемых величин с вектором оцениваемых параметров. Например, в задаче определения состояния космического аппарата в качестве оцениваемых параметров могут быть приняты параметры его орбиты: эксцентриситет, наклонение и т. д. Таким образом, в отличие от приведенных выше постановок задачи оценивания состояния динамической системы постановка задачи при использовании метода наименьших квадратов предполагает, что оцениванию подлежит некоторый r -мерный вектор неизвестных параметров
— нелинейная вектор-функция, связывающая вектор измеряемых величин с вектором оцениваемых параметров. Например, в задаче определения состояния космического аппарата в качестве оцениваемых параметров могут быть приняты параметры его орбиты: эксцентриситет, наклонение и т. д. Таким образом, в отличие от приведенных выше постановок задачи оценивания состояния динамической системы постановка задачи при использовании метода наименьших квадратов предполагает, что оцениванию подлежит некоторый r -мерный вектор неизвестных параметров 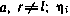 — вектор ошибок измерений, относительно которых предполагается, что математическое ожидание этих ошибок равно нулю во все моменты времени. Никакой другой априорной информации о векторе оцениваемых параметров а и ошибках измерений
— вектор ошибок измерений, относительно которых предполагается, что математическое ожидание этих ошибок равно нулю во все моменты времени. Никакой другой априорной информации о векторе оцениваемых параметров а и ошибках измерений  в принципе не требуется.
в принципе не требуется.
Предположим, что измерения проведены в моменты i = 0, 1, 2,..., N, так что в нашем распоряжении оказывается выборка из (N+1) векторов измерений уi. Введем вектор 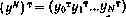 размерностью (N+1)l× 1. Тогда модель измерений для выборки из N+1 векторов yi может быть записана в виде
размерностью (N+1)l× 1. Тогда модель измерений для выборки из N+1 векторов yi может быть записана в виде

Из (3.134) следует

Будем искать оценку а* вектора параметров а из условия минимума скалярного критерия 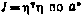 по а*:
по а*:
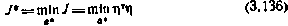
или, с учетом (3.135)
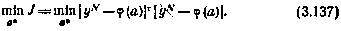
Необходимое условие минимума J по а*
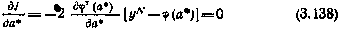
представляет собой систему из r уравнений для определения оценок а* r -мерного вектора а.
Уравнения (3.138) — нелинейные алгебраические, и их корни в общем случае следует искать численными методами. Необходимым условием существования решения системы (3.138) является требование, чтобы ранг матрицы частных производных 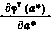 равнялся r, поскольку в противном случае система (3.138) будет неопределенной. Итак, в уравнениях (3.138) компоненты вектора а* выступают уже не как «истинные» значения оцениваемых параметров, а как варьируемые величины, среди которых есть и искомые оценки. Таким образом, в отличие от описанных выше рекуррентных байесовских алгоритмов оценивания алгоритм наименьших квадратов в его классической форме описывает способ получения оценок по полной выборке, т. е. путем одновременной обработки всей массы накопленных к данному моменту измерений. Подчеркнем также, что алгоритм наименьших квадратов не требует никаких априорных статистических сведений о динамической системе и ошибках измерений, кроме предположения о том, что среднее значение ошибок измерений равно нулю.
равнялся r, поскольку в противном случае система (3.138) будет неопределенной. Итак, в уравнениях (3.138) компоненты вектора а* выступают уже не как «истинные» значения оцениваемых параметров, а как варьируемые величины, среди которых есть и искомые оценки. Таким образом, в отличие от описанных выше рекуррентных байесовских алгоритмов оценивания алгоритм наименьших квадратов в его классической форме описывает способ получения оценок по полной выборке, т. е. путем одновременной обработки всей массы накопленных к данному моменту измерений. Подчеркнем также, что алгоритм наименьших квадратов не требует никаких априорных статистических сведений о динамической системе и ошибках измерений, кроме предположения о том, что среднее значение ошибок измерений равно нулю.
К недостатку алгоритма наименьших квадратов в приведенной выше форме следует отнести прежде всего сложность вычисления оценок, поскольку система (3.138), будучи нелинейной, может иметь в общем случае бесчисленное множество корней.
Перейдем к описанию той интерпретации метода наименьших квадратов, которая используется для определения оценок параметров движения космических аппаратов. В этом случае в качестве вектора оцениваемых параметров а может быть принят, как уже говорилось, вектор оскулирующих элементов орбиты q или вектор неизвестных начальных условий движения аппарата  . В дальнейшем [29] будем полагать, что задача оценки состояния летательного аппарата при использовании метода наименьших квадратов сводится к оценке неизвестных начальных условий его движения в момент
. В дальнейшем [29] будем полагать, что задача оценки состояния летательного аппарата при использовании метода наименьших квадратов сводится к оценке неизвестных начальных условий его движения в момент  . Предполагается также, что располагаем системой дифференциальных уравнений движения, позволяющих определять вектор состояния аппарата в любой момент
. Предполагается также, что располагаем системой дифференциальных уравнений движения, позволяющих определять вектор состояния аппарата в любой момент  при известных начальных условиях. Следующим важным предположением является допущение, что между измеряемыми величинами и оцениваемыми параметрами движения существует линейная связь, т. е.
при известных начальных условиях. Следующим важным предположением является допущение, что между измеряемыми величинами и оцениваемыми параметрами движения существует линейная связь, т. е.

где 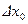 — поправка, которая вносится за счет измерений в оцениваемый n-мерный вектор начальных условий
— поправка, которая вносится за счет измерений в оцениваемый n-мерный вектор начальных условий  ;
;  — отклонения измеряемых параметров от так называемых расчетных значений (невязка измерений):
— отклонения измеряемых параметров от так называемых расчетных значений (невязка измерений):
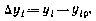
Здесь  — фактическое значение измеряемого параметра в момент
— фактическое значение измеряемого параметра в момент 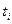 ;
; 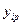 — расчетное значение измеряемого параметра в момент
— расчетное значение измеряемого параметра в момент 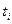 , определяемое на расчетной (опорной) траектории, соответствующей расчетным значениям начальных условий
, определяемое на расчетной (опорной) траектории, соответствующей расчетным значениям начальных условий  ;
; 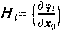
матрица l×n частных производных измеряемых параметров по компонентам вектора х0, вычисленная для опорной траектории.
В общем случае ошибки измерений характеризуются не только своим средним значением, но и разбросом относительно него, т. е. дисперсиями. Если дисперсии ошибок измерений известны при проведении соответствующих траекторных измерений, то их учитывают в алгоритме наименьших квадратов путем формирования критерия качества оценок в виде квадратичной формы

где 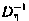 — так называемая весовая матрица, представляющая собой матрицу, обратную корреляционной матрице
— так называемая весовая матрица, представляющая собой матрицу, обратную корреляционной матрице 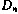 вектора ошибок измерений
вектора ошибок измерений  :
:

В (3.141)  — матрица размерности (N+1) l× ( N+1 )l. Введем теперь обозначение
— матрица размерности (N+1) l× ( N+1 )l. Введем теперь обозначение
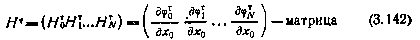
n× (N+l)l. Тогда с учетом критерия вида (3.140),.модели измерений (3.139) и введенных обозначений необходимое условие (3.138) минимума критерия по оцениваемым параметрам примет вид
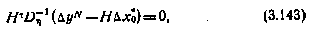
откуда
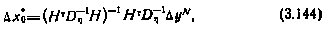
где
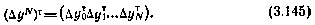
В выражениях (3.144), (3.145) 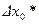 — оптимальная оценка поправок к начальным условиям, определенная по выборке yN.
— оптимальная оценка поправок к начальным условиям, определенная по выборке yN.
Система уравнений (3.143) представляет собой систему линейных алгебраических уравнений, которую можно решать, например, методом Гаусса.
При определении состояния космических аппаратов алгоритм наименьших квадратов используют многократно, в итерационном цикле, когда в качестве опорной траектории на k-й итерации используется траектория, задаваемая начальными условиями, полученными путем вычисления оценок на (k-1)-й итерации и т. д.
Таким образом, на k-й итерации имеем
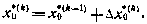
где 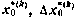 — соответственно оценка начальных условий и поправка, соответствующая k-й итерации;
— соответственно оценка начальных условий и поправка, соответствующая k-й итерации; 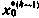 оценка начальных условий на (k-1)-й итерации. Процесс продолжается до тех пор, пока поправки
оценка начальных условий на (k-1)-й итерации. Процесс продолжается до тех пор, пока поправки 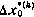 на некоторой k-й итерации не окажутся по всем компонентам меньше некоторых наперед заданных величин. Точность получаемых оценок вектора
на некоторой k-й итерации не окажутся по всем компонентам меньше некоторых наперед заданных величин. Точность получаемых оценок вектора  может быть определена из следующих соображений. Для выборки измерений объемом (N+1)l (3.139) принимает вид
может быть определена из следующих соображений. Для выборки измерений объемом (N+1)l (3.139) принимает вид

где  соответствуют (3.134), (3.142), (3.145). Умножим (3.146) слева и справа на
соответствуют (3.134), (3.142), (3.145). Умножим (3.146) слева и справа на 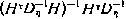 :
:
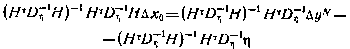
или с учетом (3.144)
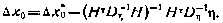
Здесь 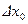 —«истинные» значения поправок к расчетным значениям начальных условий, откуда ошибка оценки
—«истинные» значения поправок к расчетным значениям начальных условий, откуда ошибка оценки
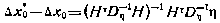
и корреляционная матрица ошибок оценки
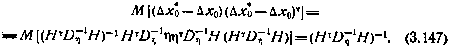
Диагональные элементы матрицы 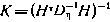 представляют собой апостериорные дисперсии компонент вектора
представляют собой апостериорные дисперсии компонент вектора 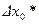 .
.
 2015-10-22
2015-10-22 878
878








