Оптимальное управление стационарным спутником с использованием импульсной корректирующей двигательной установки

Для иллюстрации методики учета изопериметрических ограничений рассмотрим задачу выбора алгоритма оптимального управления, обеспечивающего перевод стационарного искусствен­ного спутника Земли (СИСЗ) из одной точки орбиты в другую с требуемой точностью при минимальных энергетических затратах [19].

Под СИСЗ понимается ИСЗ, двигающийся в направлении вра­щения Земли по экваториальной круговой орбите с периодом об­ращения, равным периоду собственного вращения Земли. Для на­блюдателя, находящегося на Земле, такой спутник будет казаться неподвижным.

Перевод спутника предполагается осуществлять с использова­нием корректирующей двигательной установки (КДУ) большой тя­ги, позволяющей реализовать корректирующие импульсы скорости практически мгновенно. В начальный момент i=0 к СИСЗ прикла­дывается по касательной к траектории некоторый импульс скорости, в результате чего орбита движения СИСЗ становится эллиптиче­ской. Возникшая разница в периодах обращения по эллиптической и первоначальной круговой орбитам приводит к дрейфу, т. е. види­мому для земного наблюдателя смещению. Дальнейшие корректи­рующие импульсы прикладываются в моменты прохождения спут­ником точек апогея (перигея) 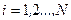и предназначаются для постепенной ликвидации дрейфа к последнему моменту N + 1 при ус­ловии обеспечения требуемой конечной точности перевода.

Введем обозначения: 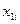— текущее угловое расстояние между i -прохождением через апогей (перигей) и требуемым положением; 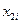— угловая скорость дрейфа в i -й момент прохождения апогея, измеряемая угловым смещением СИСЗ за один оборот; — величи­на i -гo корректирующего импульса, пересчитанная в скорость дрейфа; — случайный коэффициент с дисперсией 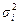, характеризующий разброс i-ro корректирующего импульса. Тогда математическая мо­дель процесса перевода может быть представлена в виде следую- щей системы конечно-разностных уравнений:

или в матричном виде

где

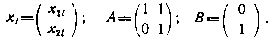
По условию задачи считается, что 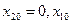— некоторая извест­ная величина.

В качестве характеристики конечной точности примем величину

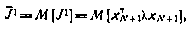
где 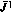— математическое ожидание (среднее значение) параметра 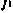эллипса

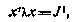
характеризующего область допустимых конечных разбросов в мо­мент N+1 в пространстве . Если К — единичная матрица, то 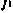является квадратом радиуса окружности рассеивания, а величина 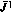— соответственно вторым моментом этого радиуса. Если кроме того допустить, что математическое ожидание вектора 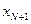равно нулю, то величина 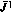будет характеризовать просто дисперсию ра­диуса рассеивания.

В процессе перевода требуется обеспечить выполнение условия

где 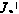заданная величина.

Энергетические затраты, подлежащие минимизации, оценим ве­личиной

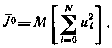
В соответствии с изложенной методикой алгоритм оптимальной коррекции может быть найден с помощью рекуррентного со­отношения (5.28), которое в данном случае принимает вид

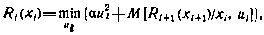
при условии

В соответствии с выражениями (5.13) — (5.17) устанавливаем, что для функции будущих потерь 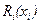имеет место формула

где матрица Λ_i определяется с помощью рекуррентного соотноше­ния

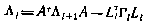
при граничном условии

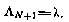
Здесь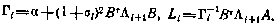

Алгоритм оптимального управления имеет вид

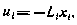
Полученные соотношения могут быть расписаны и в скалярном виде:

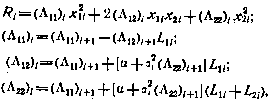
Где

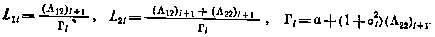
при граничных условиях

Для определения множителя установим зависимость 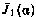. С этой целью обратимся к рекуррентному соотношению (5.26)

с граничным условием (5.27)

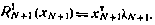
Нетрудно установить, что функция 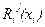, как и функция 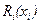, в любой момент может быть представлена в виде квадра­тичной формы

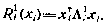
Действительно, полагая, что последнее справедливо для момента i +1, т. е.

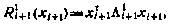
из рекуррентного соотношения для 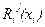находим

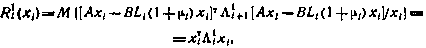
причем матрица 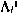связана следующим рекуррентным соотношени­ем с матрицей :

где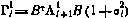

Граничное условие для 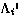имеет вид

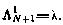
Полученные формулы в скалярном виде имеют вид

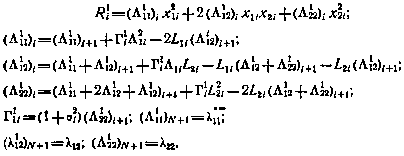
Так как начальное положение СИСЗ известно, причем х₂₀=0, то полагая i = 0 в 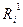, получаем оценку конечной точности

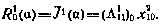
Зависимость 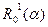проявляется через параметр (Λ₁₁¹) ₀, кото­рый, в свою очередь, зависит от множителя . Проанализируем те­перь уравнение

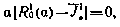
определяющее неизвестный множитель а. Можно выделить следую­щие случаи: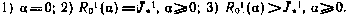

Последний случай не представляет практического интереса, так как свидетельствует о невозможности удовлетворения конечным требованиям ни при каком .

Первый случай фактически соответствует решению не исходной задачи по минимизации энергетических затрат, а задачи, связанной с достижением наилучшей конечной точности. Очевидно, если вели­чина 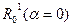, полученная в результате такого решения, окажется более заданной, 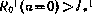, то решение исходной задачи не су­ществует. В связи с этим данный случай имеет важное значение.

С одной стороны, он дает ответ на вопрос, существует ли вообще ре­шение исходной задачи (если , то решение существу­ет, если 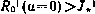, то не существует). С другой стороны, он дает представление о предельно достижимой конечной точности.

При условии существования решения можно перейти к рассмот­рению второго случая, который будет основным. Искомое значение множителя теперь определяется как положительный корень урав­нения

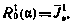
Это уравнение можно решить графически, построив зависимость 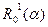при . Результаты численного решения данной задачи для различных исходных представлены в работе [19].