Границы погрешности результата измерения

В большинстве экспериментов на погрешность результата измерения с многократными наблюдениями влияют случайные погрешности и НСП. В этом случае границы погрешности результата измерения оцениваются в следующем порядке:

Пусть - граница НСП, - оценка СКО результата измерения, а - доверительная граница случайной погрешности результата измерения. Причем оценки и выполнены при одинаковой доверительной вероятности .

1. Если , то НСП пренебрегают, считая их несущественными по сравнению со случайными погрешностями, и полагают, что граница погрешности результата измерения .

2. При пренебрегают случайной погрешностью по сравнению с НСП и полагают, что граница погрешности результата измерения .

3. В случаях, когда , границу погрешности результата измерения в метрологии вычисляют путем композиции распределения случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины. Формула для вычисления границы погрешности имеет вид: , где K – коэффициент, зависящий от соотношения случайных и неисключенных систематических погрешностей; - оценка суммарного СКО результата измерения.

Коэффициент K и оценка вычисляются по формулам:

;

Однако этот способ определения границы погрешности дает явно заниженные оценки границы погрешностей .

Более правомочным полагают оценивать границу погрешности результат измерения как .

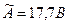Для рассматриваемых симметричных доверительных границ погрешности результат измерения величины должен представляться в виде , где . Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности . Например, если , то , но не или .

Рассмотрим вопрос об ограничении числа многократных наблюдений, применяемых при измерении физической величины.

В качестве критерия ограничения числа целесообразно использовать условие . Действительно, с ростом уменьшается , где .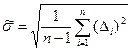

Такое уменьшение целесообразно до достижения равенства . Дальнейшее увеличение числа наблюдений не имеет смысла, поскольку при оценке границы погрешности результата измерения случайной погрешностью пренебрегают.

Поэтому максимальное число наблюдений можно оценить подстановкой в условие значения .Получаем и .