При проведении многофакторного корреляционного анализа необходимо учитывать возможность возникновения явления мультиколлениарности (явление «снежного кома»). Оно возникает тогда, когда в уравнение многофакторной зависимости включаются параметры (факторы) тесно связанные между собой. Чтобы этого избежать, в уравнения регрессии в качестве переменных должны включаться только независимые факторы. Если количество параметров x 1, x 2, … в исследовании невелико, то выделить независимые факторы можно с помощью критерия Стьюдента. Для этого:
1) составляется матрица парных коэффициентов корреляции, имеющая треугольную форму, поскольку rx 1, x 2 = rx 2, x 1;
2) для каждой пары факторов, которые включаются в уравнение, рассчитывается критерий Стьюдента t расч = │ r │ / (1 – r 2) / √ (n – 1).
Если t расч > t табл., то связь признается существенной, и из двух выделенных факторов в уравнение регрессии должен включаться лишь один.
Для практических целей количество факторов в многофакторной модели не должно превышать 6–7.
Для построения модели используют метод стандартизированного масштаба. При этом на первом этапе получают не само уравнение регрессии, а его стандартизированный вид:

Коэффициенты β в этом уравнении позволяют перейти к натуральному масштабу, а кроме того, они показывают, на какую часть своего стандартного отклонения изменяется у, если х изменится на одно стандартное отклонение. Исходя из этого, β-коэффициенты считаются аналогом показателя устойчивости и позволяют определить те параметры, которые требуют особого контроля в автоматических системах управления или дополнительных приемов стабилизации.
Для построения уравнения в стандартизированном масштабе используется матрица парных коэффициентов корреляции. На ее основе составляется система нормальных уравнений. Количество уравнений и столбцов в ней зависит от числа неизвестных:


Стандартизированное уравнение переводится в натуральный масштаб, с помощью следующих формул:
 ;
;
 ;
;
y = b 0 + b 1 x 1 + b 2 x 12 + …
Полученное уравнение регрессии требуется оценить на значимость. Оценку производят следующим образом:
1. Определяется остаточная дисперсия
 ,
,
где К – число факторов.
2. Рассчитывается критерий Фишера F = σ2 / σост2. Если F расч > F табл, то полученное уравнение хорошо описывает исследуемую зависимость. Чем больше критерий Фишера, тем более уравнение регрессии подходит для целей прогноза.
3. Рассчитывается коэффициенты множественной корреляции:
 = √ (1 – σост2 / σ2).
= √ (1 – σост2 / σ2).
4. Рассчитываются коэффициенты множественной детерминации R 2.
5. Дополнительно рассчитывается среднеквадратичная ошибка коэффициента корреляции: Sk = (1 – R) / √ (N – k – 1).
6. Определяется существенность коэффициента множественной корреляции: t расч. = R / Sk. Если t расч > t табл, то коэффициент множественной корреляции считается существенным.
Составим по этим правилам матрицу расчетных критериев Стьюдента для всех 8 исследуемых факторов х 1, х 2, …, х 8, сведенные в приведенную ниже таблицу:
| x1 | x2 | x 3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | 3,6757 | 2,6550 | 0,0280 | 0,5173 | 1,0478 | 2,5745 | 0,1641 | |
| x2 | 3,6757 | 62,2734 | 1,4791 | 0,2527 | 2,6270 | 10,8963 | 1,1329 | |
| x3 | 2,6550 | 62,2734 | 2,2296 | 0,0805 | 3,7414 | 6,4842 | 1,6404 | |
| x4 | 0,0280 | 1,4791 | 2,2296 | 1,5261 | 1,5071 | 0,4652 | 1,6365 | |
| x5 | 0,5173 | 0,2527 | 0,0805 | 1,5261 | 0,3673 | 0,3721 | 0,6368 | |
| x6 | 1,0478 | 2,6270 | 3,7414 | 1,5071 | 0,3673 | 1,2997 | 5,4576 | |
| x7 | 2,5745 | 10,8963 | 6,4842 | 0,4652 | 0,3721 | 1,2997 | 0,7004 | |
| x8 | 0,1641 | 1,1329 | 1,6404 | 1,6365 | 0,6368 | 5,4576 | 0,7004 |
Проверка на существенность и отсев второстепенных факторов производится сравнением с табличным значением t табл = 1,71. Если связь признается существенной, то из двух выделенных факторов в уравнение регрессии должен включаться лишь один. После этого можно строить многофакторную зависимость. Построим следующие две многофакторные модели (см. табл. 1 приложения):
1. Зависимость количества переработанной руды (1) от содержания металла в руде (2), содержания металла в концентрате (4), содержание серы в концентрате (5), извлечения (6).
Стандартизированный вид уравнения:
у 10 = β1 х 20 + β2 х 40 + β3 х 50 + β4 х 60 =
= –0,418 х 20 + 1,014 х 40 – 1,339 х 50 + 1,115 х 60.
Уравнение в натуральном масштабе:
y 1 = b 0 + b 1 x 2 + b 2 x 4 + b 3 x 5 + b 4 x 6 =
= 1136,08 – 122,97 х 2 + 529,16 х 4 – 17,92 х 5 + 2034,78 х 6.
Проведем оценку значимости уравнения многофакторной регрессии:
| Остаточная дисперсия | 11144,17 |
| Расчетное значение критерия Фишера F расч | 0,16 |
| Коэффициент множественной корреляции | 0,35 |
| Коэффициент множественной детерминации | 0,125 |
| Среднеквадратичная ошибка корреляции Sk | 0,168 |
| Расчетное значение критерия Стьюдента t расч | 2,14 |
| Табличное значение критерия Стьюдента t табл. | 1,70 |
| Существенность коэффициента множественной корреляции | 2,098 |
Сравнивая табличное значение критерия Стьюдента с расчетным значением, можно сделать вывод о том, что коэффициент множественной корреляции существенен. Однако значение критерия Фишера F расч = 0,16 очень мало, значит, данное уравнение нельзя использовать на практике для планирования и проектирования АСУТП. В то же время, хотя уравнение плохо описывает реальный процесс, его можно использовать для анализа.
2. Зависимость извлечения (6) от количества перерабатываемой руды (1), содержания металла в руде (2), содержания металла в хвосте (7), содержания металла в сульфате (8).
Стандартизированный вид уравнения:
у 60 = β1 х 1 0 + β2 х 20 + β3 х 70 + β4 х 80 = 0,004 4 х 10 + 1,368 х 20 +
+ 1,272 х 70 + 1,181 х 80.
Уравнение в натуральном масштабе:
у = 55,31 + 0,0003 х 1 + 43,27 х 2 – 37,34 х 7 + 2,78 х 8.
Проведем оценку значимости уравнения многофакторной регрессии:
| Остаточная дисперсия | 10,099 |
| Расчетное значение критерия Фишера F расч | 0,993 |
| Коэффициент множественной корреляции | 0,855 |
| Коэффициент множественной детерминации | 0,7307 |
| Среднеквадратичная ошибка корреляции Sk | 0,052 |
| Расчетное значение критерия Стьюдента t расч | 16,49 |
| Табличное значение критерия Стьюдента t табл. | 1,70 |
Табличное значение критерия Стьюдента значительно меньше расчетного, t расч > t табл., отсюда можно сделать вывод о том, что коэффициент множественной корреляции существенен. Значение критерия Фишера F расч = 0,993 больше по сравнению со значением критерия Фишера для первой рассмотренной зависимости, значит, последняя зависимость является более пригодной для прогноза.
В то же время, поскольку значение критерия Фишера мало, его нельзя использовать на практике для планирования и проектирования АСУТП, поскольку зависимость плохо описывает реальный процесс.
Графики и номограммы
Графики и номограммы служат для наглядного представления полученных уравнений многофакторной регрессии. Графики используются для анализа влияния каждого из входящих в уравнение факторов хi, на результирующий показатель у. Для построения графика все параметры, кроме одного, фиксируются на среднем уровне. Номограмма может быть использована как рабочий документ по двум направлениям:
– для определения уровня у по заданным уровням хi;
– для определения уровней хi по заданному уровню у.
Рассмотрим две зависимости (см. табл. 1 приложения).
1. Зависимость количества переработанной руды (1) от содержания металла в руде (2), содержания металла в концентрате (4), содержания серы в концентрате (5), извлечения (6) (рис. 8.1).
Стандартизированный вид уравнения регрессии:
у 10 = –0,418 х 20 + 1,014 х 40 – 1,339 х 50 + 1,115 х 60.
Уравнение регрессии в натуральном масштабе:
у = 1136,08 – 122,97 х 2 + 529,16 х 4 – 17,92 х 5 + 2034,78 х 6.

Рис. 8.1. Результирующий показатель
Графики на рис. 8.1 показывают, что наибольшее влияние на результирующий показатель у (количество переработанной руды) оказывает параметр х 6 (извлечение). Очень слабое влияние оказывает х 4 (содержания металла в концентрате). Негативную роль играют х 2 и х 5 (содержания металла в руде и серы в концентрате).
Для построения линий номограммы следует проанализировать β-коэффициенты в стандартизированном уравнении. Минимальное значение имеет β1, т. е. содержания металла в руде (х 20) оказывает наименьшее воздействие на выходную величину. Поэтому усредняем х 20 (х 20 = 0,58). Из оставшихся параметров находим тот, при котором β-коэффициент имеет минимальное значение. Из оставшихся параметров минимальное значение принимает β4, следовательно, содержание металла в концентрате (х 40) будет формировать линии на монограмме (рис. 8.2).
2. Зависимость извлечения (6) от (рис. 8.3) количества перерабатываемой руды (1), содержания металла в руде (2), содержания металла в хвосте (7), содержания металла в сульфате (8).
Стандартизированный вид уравнения:
у 60 = 0,004 4 х 10 + 1,368 х 20 – 1,272 х 70 – 1,181 х 80.
Уравнение регрессии в натуральном масштабе:
у = 55,31 + 0,000 3 х 1 + 43,27 х 2 – 37,34 х 7 + 2,78 х 8.

Рис. 8.2. линии номограммы:
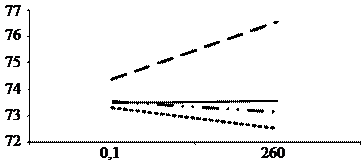
Рис. 8.3. Зависимость извлечения:
Графики на рис. 8.3, показывают, что наибольшее влияние на результирующий показатель у 6 (извлечение) оказывает параметр х 2 (содержания металла в руде). Почти не играет роли х 1 (количество переработанной руды). Малое влияние оказывает х 8 (содержание металла в сульфате), слабо негативную роль играет х 7 (содержание металла в хвосте).
Для построения линий номограммы анализируются β-коэффи-
циенты в стандартизированном уравнении. Минимальное значение имеет β1, т. е. количества перерабатываемой руды (х 10) оказывает наименьшее воздействие на выходную величину. Поэтому усредняем х 10 (х 10 = 253,68). Из оставшихся параметров находим тот, при котором β-коэффициент имеет минимальное значение, т. е. β4, следовательно. содержание металла в сульфате (х 80) будет формировать линии на монограмме (рис. 8.4).
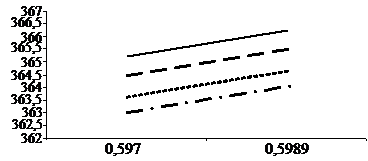
Рис. 8.4. линии номограммы
 2015-10-22
2015-10-22 419
419








