Изучаемые вопросы: Постановка задачи приближения функции. Интерполяционный многочлен Лагранжа. Оценка остаточного члена. Разделенные разности. Интерполяционная формула Ньютона. Уравнения в конечных разностях. Многочлены Чебышева. Обратная интерполяция. Ортогональные системы. Численное дифференцирование. Погрешности формул численного дифференцирования.
После изучения материала опорного конспекта и письменных лекций Вам следует решить одну из задач контрольной работы согласно «Методическим указаниям к выполнению контрольной работы. Для проверки усвоения материала Вам предстоит ответить на вопросы для самопроверки.
1.2.1.Приближение функций одной переменной
Одной из наиболее важных проблем численного анализа является проблема приближенного описания неизвестной функциональной зависимости по известным ее значениям в некоторых точках, называемых узловыми.
Задача ставится следующим образом.
Пусть функция 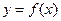 задана таблицей 1, в которой для
задана таблицей 1, в которой для 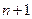 значений аргумента
значений аргумента 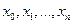 известны
известны 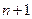 значений функции
значений функции 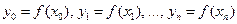 .
.
Т а б л и ц а 1
 | 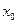 | 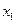 | … | 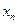 |
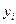 | 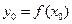 | 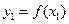 | … | 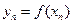 |
Требуется вычислить значения функции для значений аргумента не совпадающих с заданными в таблице. Для этого неизвестную функцию 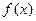 заменяют функцией
заменяют функцией 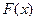 , аналитическое выражение которой известно. Эта функция
, аналитическое выражение которой известно. Эта функция 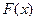 называется интерполирующей функцией, а задача её нахождения – задачей интерполяции. Точки
называется интерполирующей функцией, а задача её нахождения – задачей интерполяции. Точки 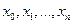 при этом называются узлами интерполяции.
при этом называются узлами интерполяции.
Таким образом, при интерполяции строится функция
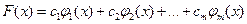 , (1)
, (1)
где 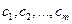 – числовые коэффициенты, которые следует определить, а
– числовые коэффициенты, которые следует определить, а 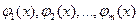 – известные функции. В качестве последних обычно используют алгебраические или тригонометрические многочлены и другие классы функций.
– известные функции. В качестве последних обычно используют алгебраические или тригонометрические многочлены и другие классы функций.
Рассмотрим некоторые методы интерполяции алгебраическими многочленами, т.е., когда интерполирующая функция – многочлен  - ой степени, значения которого в узлах совпадают со значениями интерполируемой функции.
- ой степени, значения которого в узлах совпадают со значениями интерполируемой функции.
Построим многочлен
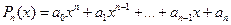 , (2)
, (2)
который будет интерполяционным, если его значения совпадают со значениями заданной функции в узлах интерполирования, т.е., если выполняется система из 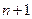 равенства
равенства
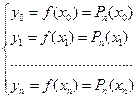 (3)
(3)
Задача состоит в вычислении коэффициентов 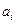 (
(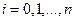 ) интерполяционного многочлена.
) интерполяционного многочлена.
Представление неизвестной функции через интерполирующую обеспечивается критериями согласия. Это либо критерий «точного совпадения в узлах», либо критерий «наименьших квадратов отклонений», либо критерий «минимума максимального отклонения».
Геометрически задачу интерполирования можно представить следующим образом.
На промежутке 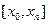 график функции
график функции 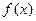 заменяется графиком многочлена
заменяется графиком многочлена 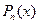 , проходящего через множество точек
, проходящего через множество точек 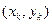 . При
. При 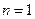 график функции
график функции 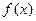 на интервале
на интервале 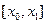 заменяется отрезком прямой (линейная интерполяция), при
заменяется отрезком прямой (линейная интерполяция), при 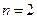 график функции
график функции 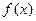 на интервале
на интервале 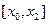 – отрезком параболы, проходящей через три точки – квадратичная интерполяция (рис. 1), где сплошная линия соответствует графику
– отрезком параболы, проходящей через три точки – квадратичная интерполяция (рис. 1), где сплошная линия соответствует графику 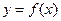 , а пунктирная – графику интерполяционного многочлена.
, а пунктирная – графику интерполяционного многочлена.
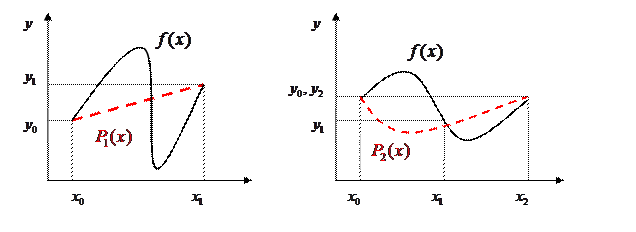
Рис.1. Интерполяция полиномами 1-й и 2-й степени.
Замечание: приближённое восстановление функции 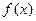 внутри минимального отрезка, содержащего все узлы интерполяции, называется интерполяцией функции, восстановление же вне этого отрезка называется экстраполяцией функции.
внутри минимального отрезка, содержащего все узлы интерполяции, называется интерполяцией функции, восстановление же вне этого отрезка называется экстраполяцией функции.
1.2.2. Интерполяционные многочлены
В общем случае интерполяционный многочлен (2), записанный в форме
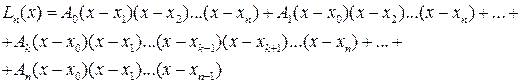 (4)
(4)
называют многочленом Лагранжа.
Коэффициенты 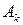 определяют из условий (3). Пусть в (4)
определяют из условий (3). Пусть в (4) 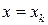 , тогда для точки
, тогда для точки 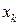
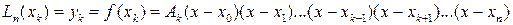 и, следовательно,
и, следовательно,
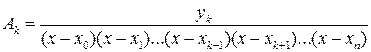 .
.
Т.е. в кратком виде полином Лагранжа можно записать так:
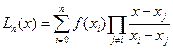 . (5)
. (5)
Можно доказать теорему:
Теорема: существует единственный интерполяционный многочлен  – ой степени, значения которого совпадают со значениями функции в узлах интерполяции.
– ой степени, значения которого совпадают со значениями функции в узлах интерполяции.
Поэтому, имея 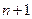 узел, можно построить интерполяционный многочлен степени
узел, можно построить интерполяционный многочлен степени  .
.
Рассмотрим случай, когда узлы интерполирования равно отстоят друг от друга, т.е. 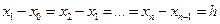 . Конечными разностями первого порядка функции
. Конечными разностями первого порядка функции 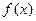 называются выражения
называются выражения
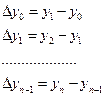 ,
,
а в общем виде, разности первого порядка
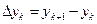 , где
, где 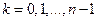 . (6)
. (6)
Конечные разности второго порядка
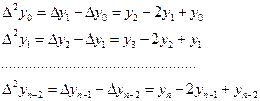 ,
,
или, в общем виде, разности второго порядка
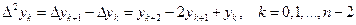 . (7)
. (7)
Аналогично, разность порядка m определяется формулой

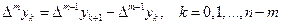 . (8)
. (8)
Вычисление разностей удобно оформлять в виде таблицы (см. табл.2). Каждый элемент таблицы получается вычитанием элемента этой же строки из элемента последующей строки предыдущего столбца.
Т а б л и ц а 2
 |  |  | 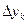 | 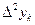 | 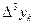 | 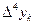 | 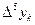 |
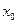 | 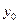 | 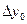 | 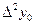 | 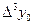 | 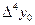 | 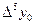 | |
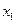 | 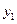 | 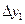 |  | 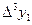 | 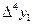 | --- | |
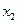 | 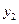 | 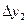 | 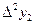 | 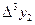 | --- | --- | |
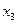 | 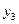 | 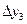 | 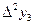 | --- | --- | --- | |
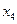 | 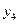 | 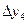 | --- | --- | --- | --- | |
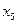 |  | --- |
| x | ||||
| y |
Пример: функция 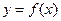 задана таблицей
задана таблицей
(Назовём эти данные экспериментальными).
Составить таблицу конечных разностей.
Результаты сведены в таблицу, содержащую разности до третьего порядка включительно.
 |  |  | 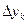 | 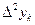 | 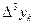 |
Действительно, 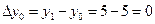 ,
,
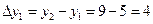 ,
, 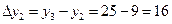 ,
,
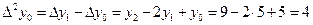 ,
,
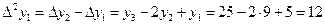 ,
,
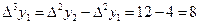 .
.
Если узлы интерполирования равноотстоящие, т.е. 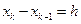 , где
, где 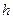 – шаг интерполирования (а в нашем примере это так), то удобно искать интерполяционный многочлен в виде многочлена Ньютона:
– шаг интерполирования (а в нашем примере это так), то удобно искать интерполяционный многочлен в виде многочлена Ньютона:
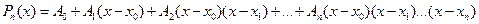 . (9)
. (9)
Коэффициенты 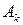 при этом рассчитываются по формуле
при этом рассчитываются по формуле
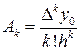 . (10)
. (10)
1.2.3. Численное дифференцирование
Простейшие формулы численного дифференцирования получают в результате дифференцирования интерполяционных формул.
Допустим, известны значения функции 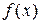 в узлах
в узлах 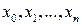 . Требуется вычислить производную
. Требуется вычислить производную 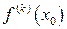 . Строим интерполяционный многочлен
. Строим интерполяционный многочлен 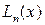 и полагаем, что
и полагаем, что 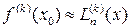 . Т.е. значения производных функции принимаются приближённо равными производным соответствующего порядка от многочлена интерполяции.
. Т.е. значения производных функции принимаются приближённо равными производным соответствующего порядка от многочлена интерполяции.
При аппроксимации функции интерполяционным многочленом Ньютона
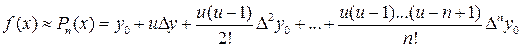 , (11)
, (11)
где 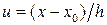 . Введём обозначение
. Введём обозначение
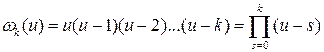 , (12)
, (12)
тогда интерполяционный многочлен Ньютона примет вид
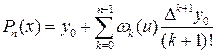 , (13)
, (13)
и, дифференцируя это выражение, получим
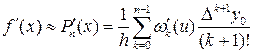 , (14)
, (14)
а т.к. 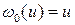 и
и 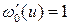 , то
, то
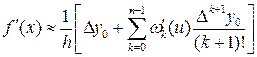 . (15)
. (15)
Аналогично, формула для второй производной будет:
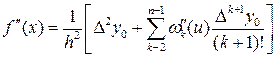 . (16)
. (16)
Из полученных формул следует, что основная сложность состоит в нахождении производных  и
и 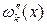 .
.
Получим расчётную формулу для первой производной  :
:
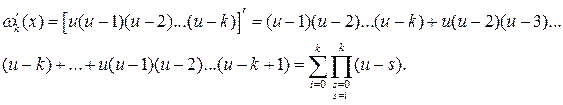
Теперь пусть 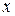 совпадает с одним из узлов интерполирования. Тогда все слагаемые, кроме одного, не содержащего разности
совпадает с одним из узлов интерполирования. Тогда все слагаемые, кроме одного, не содержащего разности 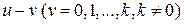 будут равны нулю. И
будут равны нулю. И
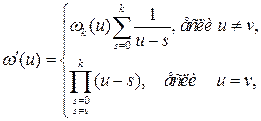 (17)
(17)
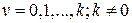 .
.
Полученные формулы позволяют вычислить приближённые значения производной при любом количестве узлов. В частности, при двух узлах интерполирования (линейная интерполяция)
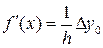 . (18)
. (18)
При трёх узлах интерполирования (квадратичная интерполяция)
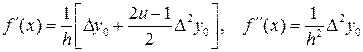 . (19)
. (19)
При наличии четырёх узлов интерполирования формулы для производных примут вид:
 (20)
(20)
Если производная вычисляется в нулевом узле, то 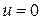 и формулы (20) приобретают вид:
и формулы (20) приобретают вид:
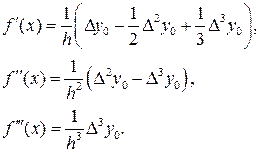 (21)
(21)
Ошибка при вычислении производных существенно увеличивается при увеличении порядка производной, поэтому обычно для вычисления производных порядка выше третьего этот метод не используется.
Более полное изложение этой темы Вы можете найти в [5], c.35-85.
Вопросы для самопроверки по теме 1.2
1. В чём состоит задача интерполяции функции?
2. Какие критерии согласия обеспечивают совпадение неизвестной функции с интерполирующей?
3. Как называется интерполяция многочленами первой и второй степени?
4. Напишите общие формулы конечных разностей 1-го, 2-го и 3-го порядков.
5. Напишите формулу интерполяционного многочлена Ньютона для пяти узлов.
6. Чему равна третья производная 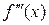 при трёх узлах интерполирования?
при трёх узлах интерполирования?
 2015-10-22
2015-10-22 2873
2873








