Из всех вопросов темы 1.6. Численные методы алгебры, изучается вопрос о приближённом решении уравнений.
После изучения материала опорного конспекта и письменных лекций Вам следует решить одну из задач контрольной работы согласно «Методическим указаниям к выполнению контрольной работы «Численные методы и инженерные расчёты» (с.74).
Приближённое вычисление корней уравнения 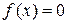
В общем случае задача отыскания точных значений корней уравнения 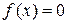 неразрешима. Даже для алгебраических уравнений выше третьей степени нет решений в виде формул с конечным числом арифметических действий.
неразрешима. Даже для алгебраических уравнений выше третьей степени нет решений в виде формул с конечным числом арифметических действий.
Сформулируем задачу следующим образом:
Дано уравнение
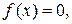 (1)
(1)
где 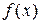 - непрерывная функция в области
- непрерывная функция в области 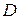 . Корни этого уравнения
. Корни этого уравнения 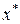 – это те значения аргумента
– это те значения аргумента 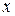 , которые обращают уравнение (1) в тождество. Найти приближённое значение корня
, которые обращают уравнение (1) в тождество. Найти приближённое значение корня 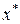 с точностью
с точностью  означает указать интервал длиной не более
означает указать интервал длиной не более  , содержащий точное значение корня
, содержащий точное значение корня 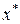 .
.
Решение этой задачи состоит из двух этапов:
1. Отделение корня, т.е. выделение отрезка  из области непрерывности функции
из области непрерывности функции 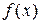 , содержащего только один корень уравнения (1).
, содержащего только один корень уравнения (1).
2. Уточнение корня, т.е. построение итерационного процесса, позволяющего сколь угодно сузить границы выделенного интервала до значения заданной точности. Первоначальные границы его можно рассматривать как нулевое приближение искомого корня ( – с недостатком,
– с недостатком, 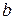 – с избытком).
– с избытком).
Для отделения корней уравнения (1) нужно знать те условия, которые позволяют утверждать, что, во-первых, на промежутке  есть корень уравнения, а во-вторых, что он единственный на этом промежутке. Здесь следует иметь в виду следующее.
есть корень уравнения, а во-вторых, что он единственный на этом промежутке. Здесь следует иметь в виду следующее.
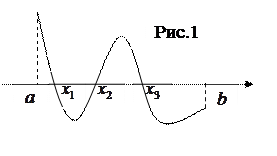
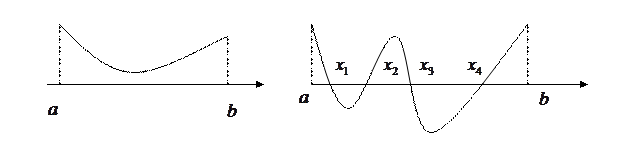
1. Если 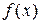 непрерывна на
непрерывна на  и имеет на концах промежутка разные знаки, то на
и имеет на концах промежутка разные знаки, то на  существует нечётное количество корней. На рис.1 кривая соответствует функции
существует нечётное количество корней. На рис.1 кривая соответствует функции  , а точки
, а точки 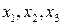 – точки пересечения графика функции с осью абсцисс – корни уравнения
– точки пересечения графика функции с осью абсцисс – корни уравнения 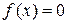 . Т.о., разные знаки функции на концах промежутка обеспечивают наличие корня на
. Т.о., разные знаки функции на концах промежутка обеспечивают наличие корня на  , но не гарантируют его единственности.
, но не гарантируют его единственности.
2. Если 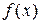 непрерывна на
непрерывна на  и имеет на концах промежутка одинаковые знаки, то, как правило, на этом промежутке число корней чётно, в том числе и 0, т.е. они могут и отсутствовать (рис.2 а, б).
и имеет на концах промежутка одинаковые знаки, то, как правило, на этом промежутке число корней чётно, в том числе и 0, т.е. они могут и отсутствовать (рис.2 а, б).
а) б)
Рис.2
Однако нельзя не учитывать, что корнем функции может быть не только точка пересечения графика  с осью ОХ, но и точка касания с осью (рис.3 а, б, в). Заметим, что в этих случаях в точке
с осью ОХ, но и точка касания с осью (рис.3 а, б, в). Заметим, что в этих случаях в точке 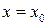 нарушается монотонность функции
нарушается монотонность функции 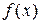 .
.
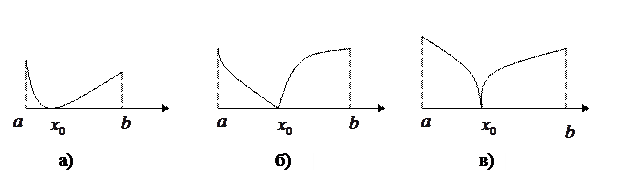
Рис.3
Таким образом, можно сформулировать следующий достаточный критерий для отделения корня: если на интервале  функция
функция 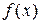 непрерывна, монотонна и её значения на концах интервала имеют разные знаки, то на
непрерывна, монотонна и её значения на концах интервала имеют разные знаки, то на  существует один и только один корень уравнения (1).
существует один и только один корень уравнения (1).
Из этого критерия следует, что для единственности корня на  достаточно, чтобы выполнялось условие
достаточно, чтобы выполнялось условие 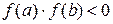 , а производная этой функции
, а производная этой функции 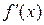 была бы знакопостоянна при любом
была бы знакопостоянна при любом  (рис.4 а, б).
(рис.4 а, б).
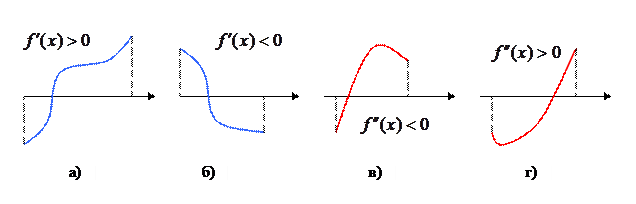
Замечание 1. Для единственности корня на  при
при 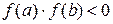 бывает достаточно и знакопостоянства второй производной
бывает достаточно и знакопостоянства второй производной  (рис.4 в, г).
(рис.4 в, г).
|
Итак, для того, чтобы отделить все вещественные корни уравнения (1), достаточно найти все интервалы монотонности 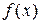 , т.к. на каждом из этих интервалов может быть не более одного корня. Если на интервале монотонности
, т.к. на каждом из этих интервалов может быть не более одного корня. Если на интервале монотонности 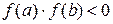 , то корень есть, если
, то корень есть, если 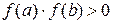 , то корня нет. Интервалы монотонности соответствуют интервалам знакопостоянства
, то корня нет. Интервалы монотонности соответствуют интервалам знакопостоянства 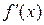 .
.
Замечание 2. Следует рассмотреть те случаи, когда 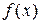 имеет одинаковые знаки на концах интервала, и, тем не менее, на нём существует корень (см. рис.3). Заметим, что в точках
имеет одинаковые знаки на концах интервала, и, тем не менее, на нём существует корень (см. рис.3). Заметим, что в точках 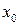 , соответствующих корню, производная
, соответствующих корню, производная 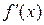 либо не существует, либо равна нулю, либо
либо не существует, либо равна нулю, либо 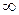 , т.е. в этих точках
, т.е. в этих точках 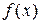 достигает экстремума и, следовательно, корень является границей монотонности.
достигает экстремума и, следовательно, корень является границей монотонности.
Т.о., чтобы отделить все корни уравнения (1) следует: 1) найти промежуток, где 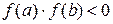 , а
, а 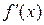 или
или  , или обе производные знакопостоянны; 2) отыскать нули и точки разрыва
, или обе производные знакопостоянны; 2) отыскать нули и точки разрыва 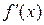 и проверить, не являются ли они корнями уравнения (1).
и проверить, не являются ли они корнями уравнения (1).
Пример. Отделить все вещественные корни уравнения  . Имеем:
. Имеем: 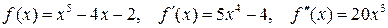 . Здесь
. Здесь 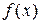 непрерывна, поэтому для определения её интервалов монотонности достаточно найти нули производной
непрерывна, поэтому для определения её интервалов монотонности достаточно найти нули производной 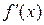 :
: 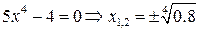 . Таким образом, отделяются три промежутка монотонности
. Таким образом, отделяются три промежутка монотонности 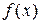 и, следовательно, имеется не более трёх корней на следующих промежутках:
и, следовательно, имеется не более трёх корней на следующих промежутках:

При этом 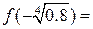 1.026373149,
1.026373149, 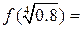 -5.026373149, следовательно, на промежутке
-5.026373149, следовательно, на промежутке  есть единственный корень.
есть единственный корень.
Чтобы отделить два оставшихся корня, вычислим  , тогда на промежутке
, тогда на промежутке 
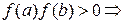 корня нет.
корня нет.  на интервале (-2; -1) есть единственный корень. Аналогично, на интервале
на интервале (-2; -1) есть единственный корень. Аналогично, на интервале 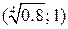 корня нет, а на интервале [1; 2] – также единственный корень. Графики
корня нет, а на интервале [1; 2] – также единственный корень. Графики 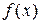 и её первой и второй производной – рис.5 а), б), в).
и её первой и второй производной – рис.5 а), б), в).
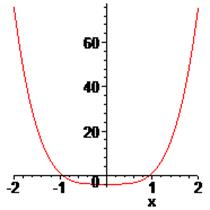
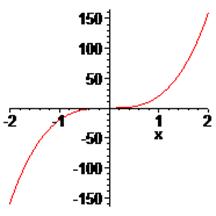

а) б) в)
Рис.5
О методах отделения корней Вы можете прочитать подробнее в [2, Раздел 4].
Вопросы для самопроверки по теме 1.6
1. Можно ли в общем случае найти корни уравнения 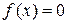 ?
?
2. Какие этапы следует пройти при вычислении корней уравнения 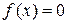 ?
?
3. Каково условие единственности корня на отрезке  ?
?
 2015-10-22
2015-10-22 457
457








