«Методические указания» изданы отдельно (см. [9]).
Раздел 4. БЛОК КОНТРОЛЯ ОСВОЕНИЯ ДИСЦИПЛИНЫ
Методические указания к выполнению контрольных работ
Контрольные работы №1 и №2
Студенты всех специальностей разделены на три группы и выполняют задания двух контрольных работ в соответствии с таблицей, приведённой ниже (задания имеют сквозную нумерацию по обеим контрольным работам).
| Группа № | Специальности № | Задания № |
| 140211, 140101, 140104,150501, 190205, 200101, 220201 | 1 (интерполяция) 2 (корни уравнения) 5 (комплексные числа) 6 (производная ФКП) 7 (интегрирование ФКП) 8 (алгоритм Дейкстры) 9 (мат. логика) | |
| 080502, 150104, 151001, 150202, 190601, 140601, 200402, 200501, 210106, 210302, 210101, 220301, 230101, 280202 | 1 (интерполяция) 2 (корни уравнения) 3 (численное интегрирование) 4 (метод Эйлера) 5 (комплексные числа) 6 (производная ФКП) 7 (интегрирование ФКП) | |
| 190701*), 240401, 240301 | 5 (комплексные числа) 6 (производная ФКП) 7 (интегрирование ФКП) 8 (алгоритм Дейкстры) 9 (мат. логика) |
*)Студенты специальности 190701 выполняют также два задания из УМК "Математика ч.2 Методы оптимизации". Номера заданий указывает преподаватель.
Варианты индивидуальных заданий
Задание 1. Осуществить интерполяцию с помощью полинома Ньютона исходных данных из табл.1 и вычислить значение интерполяционного полинома в точке 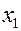 . Номер варианта выбирается по последней цифре шифра. 10 точек берётся, если для решения задачи используется какой-либо математический пакет. При ручном счёте – выбрать первые четыре точки.
. Номер варианта выбирается по последней цифре шифра. 10 точек берётся, если для решения задачи используется какой-либо математический пакет. При ручном счёте – выбрать первые четыре точки.
Таблица 1
| Порядковый номер исходных данных | ||||||||||
| № | ||||||||||
| 1-й вариант | ||||||||||
| Х | 1,415 | 1,420 | 1,425 | 1,430 | 1,435 | 1,440 | 1,445 | 1,450 | 1,455 | 1,460 |
| У | 0,888 | 0,889 | 0,890 | 0,891 | 0,892 | 0,893 | 0,894 | 0,895 | 0,896 | 0,897 |
| Значение | х 1 = 1,416 | |||||||||
| 2-й вариант | ||||||||||
| Х | 0,101 | 0,106 | 0,111 | 0,116 | 0,121 | 0,126 | 0,131 | 0,136 | 0,141 | 0,146 |
| У | 1,261 | 1,276 | 1,291 | 1,306 | 1,321 | 1,336 | 1,352 | 1,367 | 1,383 | 1,399 |
| Значение | х 1 = 0,113 | |||||||||
| 3-й вариант | ||||||||||
| Х | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | 0,55 | |
| У | 0,86 | 0,819 | 0,779 | 0,741 | 0,705 | 0,670 | 0,638 | 0,606 | 0,577 | 0,549 |
| Значение | х 1 = 0,23 | |||||||||
| 4-й вариант | ||||||||||
| Х | 0,18 | 0,185 | 0,190 | 0,195 | 0,200 | 0,205 | 0,210 | 0,215 | 0,220 | 0,225 |
| У | 5,615 | 5,467 | 5,352 | 5,193 | 5,066 | 4.946 | 4,832 | 4,722 | 4,618 | 4,519 |
| Значение | х 1 = 0,182 | |||||||||
| 5-й вариант | ||||||||||
| Х | 3,5 | 3,55 | 3,60 | 3,65 | 3,70 | 3,75 | 3,80 | 3,85 | 3,90 | 3,95 |
| У | 33,11 | 34,65 | 36,60 | 38,47 | 40,44 | 42,52 | 44,70 | 46,99 | 49,40 | 51,93 |
| Значение | х 1 = 3,52 | |||||||||
| 6-й вариант | ||||||||||
| Х | 0,115 | 0,120 | 0,125 | 0,130 | 0,135 | 0,140 | 0,145 | 0,150 | 0,165 | 0,170 |
| У | 8,68 | 8,29 | 7,96 | 7,65 | 7,36 | 7,10 | 6,85 | 6,62 | 6,40 | 6,20 |
| Значение | х 1 = 0,122 | |||||||||
| 7-й вариант | ||||||||||
| Х | 1,340 | 1,345 | 1,350 | 1,355 | 1,360 | 1,365 | 1,370 | 1,375 | 1,380 | 1,385 |
| У | 4,26 | 4,35 | 4,46 | 4,56 | 4,67 | 4,79 | 4,91 | 5,01 | 5,18 | |
| Значение | х 1 = 1,352 | |||||||||
| 8-й вариант | ||||||||||
| Х | 0,15 | 0,16 | 0,17 | 0,18 | 0,19 | 0,20 | 0,21 | 0,22 | 0,23 | 0,24 |
| У | 4,48 | 4,95 | 5,47 | 5,99 | 6,05 | 6,68 | 6,909 | 7,38 | 8,166 | 9,025 |
| Значение | х 1 = 0,153 | |||||||||
| 9-й вариант | ||||||||||
| Х | 0,45 | 0,46 | 0,47 | 0,48 | 0,49 | 0,50 | 0,51 | 0,52 | 0,53 | 0,54 |
| У | 20,19 | 19,61 | 18,94 | 18,17 | 17,30 | 16,31 | 15,19 | 13,94 | 12,55 | 10,99 |
| Значение | х 1 = 0,455 | |||||||||
| 10-й вариант | ||||||||||
| Х | 0,01 | 0,06 | 0,11 | 0,16 | 0,21 | 0,26 | 0,31 | 0.36 | 0,41 | 0,46 |
| У | 0,99 | 0,95 | 0.91 | 0,88 | 0,84 | 0,81 | 0,78 | 0,74 | 0,71 | 0,68 |
| Значение | х 1 = 0,014 |
Задание 2. Уточнить значение корня на заданном интервале тремя итерациями и найти погрешность вычисления. Номер варианта выбирается по предпоследней цифре шифра из табл.2.
Таблица 2
| Номер варианта | Уравнение | Интервал |
| 2 х 3 - 5 х 2 + 4 х - 9 = 0 | [ 0;4 ] | |
| 3 х 3 - 10 х 2 +2 х - 7 = 0 | [ 0;4 ] | |
| 3 х 3 - 7 х 2 +2 х - 5 = 0 | [-1;3 ] | |
| 2 х 3 – 5 х 2 + 5 х - 12 = 0 | [ 0;4 ] | |
| 5 х 3 - 3 х 2 + 4 х -12 = 0 | [ 0;4 ] | |
| 2 х 3 - 5 х 2 +5 х - 12 = 0 | [ 2;6 ] | |
| 2 х 3 - 5 х 2 +4 х - 11 = 0 | [ 2;6 ] | |
| 2 х 3 - 7 х 2 + 3 х - 10 = 0 | [ 0;4 ] | |
| 3 х 3 - 105 х 2 + 2 х - 7= 0 | [ 2;6 ] | |
| 3 х 3 - 2 х 2 +5 х - 3= 0 | [ -2;2 ] |
Задание 3. Методами прямоугольников, трапеций и Симпсона вычислить определённый интеграл. Номер варианта выбирается по предпоследней цифре шифра.
1)  2)
2) 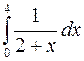 3)
3) 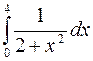 4)
4)  5)
5) 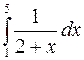
6)  7)
7) 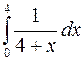 8)
8) 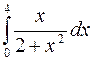 9)
9) 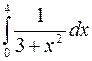 10)
10) 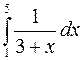
Задание 4. Проинтегрировать уравнение методом Эйлера на интервале 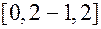 . Во всех вариантах начальное условие:
. Во всех вариантах начальное условие: 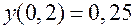 . Вычисления выполнять с четырьмя десятичными знаками и шагом
. Вычисления выполнять с четырьмя десятичными знаками и шагом 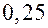 . Номер варианта выбирается по последней цифре шифра.
. Номер варианта выбирается по последней цифре шифра.
1) 
2) 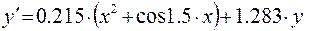
3) 
4) 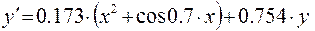
5) 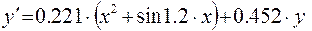
6) 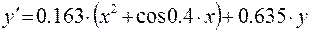
7) 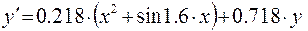
8) 
9) 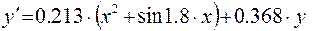
10) 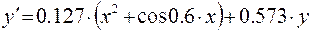
Задание 5. Данное задание состоит из двух задач. В первой из них требуется вычислить сумму (z 1+ z 2) и разность (z 1 - z 2) комплексных чисел, а во второй – произведение z 1 z 2 и частное z 1 /z 2.
Вариант задания выбирается по последней цифре шифра.
Заданча 1. В задании 1-10, вычислить сумму (z 1+ z 2) и разность (z 1- z 2) комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму; построить операнды и результаты на комплексной плоскости.
Заданча 2. В задании 11-20 вычислить произведение z 1 z 2 и частное z 1 /z 2комплексных чисел, операнды и результаты изобразить на комплексной плоскости.
1. 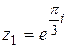 ; ; 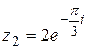 . .
| 6. 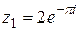 ; ; 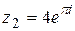 . .
|
2. 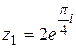 ; ; 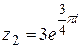 . .
| 7. 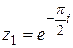 ; ;  . .
|
3.  ; ; 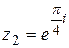 . .
| 8. 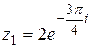 ; ;  . .
|
4. 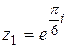 ; ; 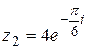 . .
| 9. 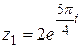 ; ; 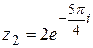 . .
|
5. 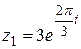 ; ; 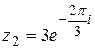 . .
| 10. 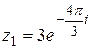 ; ;  . .
|
11. 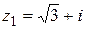 ; ; 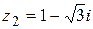 . .
| 16. 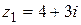 ; ; 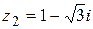 . .
|
12. 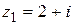 ; ; 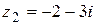 . .
| 17. 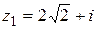 ; ;  . .
|
13. 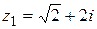 ; ;  . .
| 18. 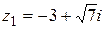 ; ;  . .
|
14.  ; ; 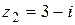 . .
| 19. 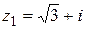 ; ; 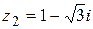 . .
|
15. 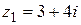 ; ;  . .
| 20.  ; ; 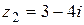 . .
|
Задание 6. Вачислить производную функции 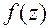 в точке
в точке  . Номер задания выбрать по предпоследней цифре шифра.
. Номер задания выбрать по предпоследней цифре шифра.
1.   . .
| 6. 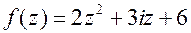 ; ; 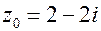 . .
|
2.   . .
| 7. 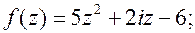 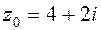 . .
|
3. 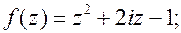  . .
| 8.  ; ;  . .
|
4. 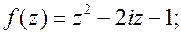  . .
| 9.  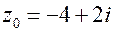 . .
|
5. 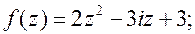 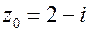 . .
| 0. 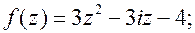 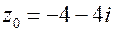 . .
|
Задание 7. Вычислить интеграл по замкнутым контурам а) и б), считая обход контура в положительном направлении. Нарисовать область интегрирования, указать на рисунке особые точки. Номер задания выбрать по последней цифре шифра.
31. 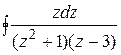 ; ;
| а) 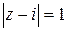 , ,
| б)  . .
|
32. 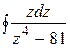 ; ;
| а)  , ,
| б) 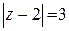 . .
|
33. 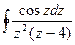 ; ;
| а) 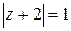 , ,
| б)  . .
|
34. 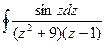 ; ;
| а) 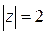 , ,
| б) 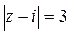 . .
|
35. 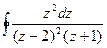 ; ;
| а) 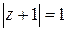 , ,
| б)  . .
|
36. 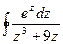 ; ;
| а) 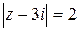 , ,
| б) 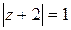 . .
|
37.  ; ;
| а) 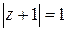 , ,
| б) 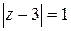 . .
|
38.  ; ;
| а) 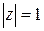 , ,
| б) 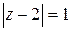 . .
|
39.  ; ;
| а)  , ,
| б) 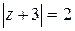 . .
|
40.  ; ;
| а) 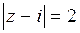 , ,
| б) 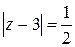 . .
|
Задание 8. 1. По заданной матрице весов построить граф и найти кратчайший путь между вершинами  и
и 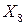 , используя алгоритм Дейкстры.
, используя алгоритм Дейкстры.
2. С помощью алгоритма ближайшего соседа определить минимальное остовное дерево в рассматриваемом графе.
Вариант задания выбирается по последней цифре шифра:
1)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
2)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
3)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
4)
5)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
6)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
7)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
8)
9)
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
10)
Задание 9. Для исходной булевой функции, заданной таблицей найти сокращённую ДНФ методом Квайна.
Вариант задания выбирается по последней цифре шифра:
| № варианта | ||||||||||||
| x | y | z | Значения функции | |||||||||
 2015-10-22
2015-10-22 425
425








