Элементы алгебры логики

Изучаемые вопросы: Высказывания. Основные логические операции. Булевы функции и нормальные формы. Совершенные дизъюнктивная и конъюнктивная нормальные формы. Полные системы булевых функций и базис. Нахождение сокращённой дизъюнктивной нормальной формы (ДНФ) методом Квайна. Построение минимальных ДНФ методом Петрика. Технические применения алгебры логики.

3.3.1. Основные логические операции

1. Отрицание высказывания – это операция, выражающая высказывание, которое истинно, если исходное высказывание ложно, и наоборот. Обозначают его чертой сверху или знаком . Называется также инверсией или дополнением к 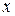. Таблица истинности для отрицания:

2. Конъюнкция двух высказываний – это высказывание, которое истинно тогда и только тогда, когда оба высказывания истинны (и ложно, когда ложно хотя бы одно). Это т.н. логическое умножение: 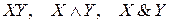( – логическое «и», & - амперсанд, или коммерческое «и»).

3. Дизъюнкция двух высказываний – это высказывание, которое истинно тогда и только тогда, когда, по крайней мере, одно из них истинно (и ложно, когда оба ложны): ( 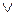– логическое «или») – это логическое сложение.

Таблица истинности для этих двух операций выглядит так:

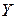Примеры. 1. Пусть высказывания –параллелограмм (см. рисунок) – это пример конъюнкции.

2. Пример дизъюнкции: делится на 2, делится на 2. Тогда высказывание – чётное число.

3. Эквиваленция двух высказываний – это высказывание, которое истинно тогда и только тогда, когда значения истинности A и В совпадают: А ~ В.

4. Импликацией двух высказыванийназывается высказывание, которое ложно тогда и только тогда, когда значение истинности первого аргумента – “истина”, а второго – “ложь”. Обозначается: x ₁ ® x ₂. Читается: “импликация x ₁ в x ₂”, “ x ₁ влечет x ₂”.

5. Сложением по модулю два называется функция, принимающая значение истинности “истина”, если аргументы имеют разные значения истинности, и “ложь”, если аргументы имеют одинаковые значения истинности. Обозначается: x ₁ Å x ₂; читается: “сложение по модулю два x ₁ и x ₂”.

Таблица истинности для этих двух операций выглядит так:

Свойства элементарных логических операций:

1.Коммутативность: .

2. Идемпотентность: .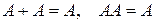

3. Ассоциативность: .

4. Дистрибутивность: .

5. Формулы Моргана: .

6. .

3.3.2. Булевы функции и нормальные формы

Булевой функцией называется произвольная -местная функция двоичных аргументов , т.е. аргументы её принимают значения 0 и 1, и функция принимает такие же значения – 0 и 1.

Всякую булеву функцию от переменных можно задать таблицей из строк, в которой в каждой строке записывают одно из значений этих переменных 0 или 1.

Т.к. длина каждого столбца равна , а различных столбцов из 0 и 1 длины имеется 2 в степени , то существует ровно различных -местных булевых функций. Например, для булевой функции от двух аргументов имеется различных булевых функций:

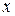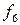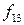Здесь, кстати, называется функцией Шафера, а – функцией Вебба.

Ясно, что для одноместной булевой 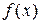имеется 4 функции, а для 3-местной 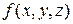– 256 функций.

В алгебре логики доказывается, что всякую булеву функцию можно представить в виде некоторого числа конъюнктивных членов, образованных её аргументами или их отрицаниями, соединённых знаками дизъюнкции.

Эта форма представления булевой функции называется совершенной дизъюнктивной нормальной формой (СДНФ).

Правило построения СДНФ булевой функции, заданной таблицей, состоит в следующем:

1. Из таблицы выбираем все наборы аргументов , для которых .

2. Для каждого из этих наборов составляем конъюнкции, равные 1.

3). Все эти конъюнкции соединяем знаками дизъюнкции.

Пример 1. Составить СДНФ для 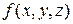, заданной табл. 1:

Табл.1. Функция .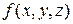

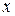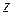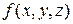1. Отметим строки, где (их 5).

2. Для этих наборов конъюнкции, равные 1 будут такими (см. табл. истинности для конъюнкции):

3. Соединяя их знаками дизъюнкции, получаем искомую СДНФ: .

Отметим, что конъюнктивные члены, входящие в СДНФ, называются конституантами единицы.

Аналогично понятию СДНФ вводится совершенная конъюнктивная нормальная форма (СКНФ), которая может быть представлена в виде некоторого числа дизъюнктивных членов, соединённых знаками конъюнкции. Правило составления СКНФ булевой функции, заданной таблицей, формулируется так:

1. Выбираются все наборы, для которых .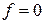

2. Для каждого из этих наборов составляются дизъюнкции, равные 0.

3. Полученные дизъюнкции соединяются знаками конъюнкции.

В том же примере: 1) Это будут строки 2, 4, 5, и, т.к. дизъюнкция равна нулю, когда оба высказывания равны 0, то 2) нулевые дизъюнкции будут: . Тогда СКНФ:

.

Отметим, что дизъюнктивные члены, входящие в СКНФ, называются конституантами нуля.

3.3.3. Полные системы булевых функций и базис

Система булевых функций называется полной, если любую булеву функцию можно представить в виде формулы через функции .

Сама система функций при этом называется базисом.

Базис минимален, если удаление хотя бы одной из входящих в него функций, превращает систему их в неполную.

Выше мы отметили, что любую булеву функцию можно представить через отрицания, конъюнкции и дизъюнкции, следовательно, система функций является базисом. Однако этот базис не является минимальным, т.к. на основании формул Моргана из него можно удалить одну из функций – дизъюнкцию, или конъюнкцию, не нарушив его полноты. Значит, в качестве базиса можно взять любую из систем функций: или 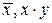, поскольку инверсия не выражается через конъюнкцию или дизъюнкцию, и каждый из этих базисов будет минимальным. Т.о., существует несколько различных базисов, и выбор его определяется характером рассматриваемой задачи. Подробнее о минимальных формах – в учебнике.

3.3.4. Нахождение сокращённой ДНФ

Рассмотрим процедуру построения сокращённой ДНФ методом Квайна. Он основан на преобразовании ДНФ с помощью операций полного и неполного склеивания и операции поглощения.

Введём ещё одно понятие: конъюнкция переменных называется элементарной, если каждая из этих переменных встречается в конъюнкции не более одного раза.

Пусть 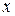– булева переменная, а – элементарная конъюнкция. Тогда имеет место равенство:

(1)

○ ●

Это соотношение называется соотношением полного склеивания, т.е. в дизъюнкции члены и склеиваются по .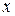

Имеет место также соотношение неполного склеивания:

(2)

○ используя свойство идемпотентности получаем:

, но ●

Теперь, наряду с элементарной конъюнкцией , рассмотрим ещё одну – , тогда имеет место соотношение поглощения:

(3)

○ ●

Если в случае полного склеивания говорят, что члены и склеиваются по 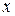, то в случае поглощения в дизъюнкции член поглощается членом .

По теореме Квайна, если в СДНФ вначале произвести все операции неполного склеивания, а затем все операции поглощения, то в результате получим сокращённую ДНФ.

Приведём алгоритм построения сокращённой ДНФ методом Квайна.

1. Найти СДНФ заданной 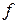. В ней все конъюнктивные члены будут иметь один ранг (ранг равен числу членов в конъюнкции).

2. Провести в ДНФ все возможные операции неполного склеивания. Их удобно проводить в два этапа: сначала все возможные операции полного склеивания, а затем выписать результаты полного склеивания в начале ДНФ, соединив их между собой и с остальными членами ДНФ знаками дизъюнкции (это и будет неполное склеивание).

3. Провести все возможные операции поглощения, в результате чего получим ДНФ, состоящую из элементарных конъюнкций ранга, на единицу меньшего.

4. В полученной ДНФ провести все возможные операции склеивания и поглощения в соответствии с п.3) и 4). В результате получим ДНФ, состоящую из элементарных конъюнкций ранга ещё на единицу меньшего.

Описанную процедуру следует проводить до тех пор, пока это будет возможно. Полученная в итоге ДНФ и будет сокращённой. Образующие её элементарные конъюнкции называются простыми импликантами функции .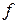

Пример 1. Найти сокращённую ДНФ булевой функции

□

1. Здесь первый конъюнктивный член имеет ранг, равный двум, а остальные – 3. Приведём все члены к одному рангу, равному трём. Для этого умножим первый член на 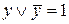. Получаем:

(4)

2. Проведём все возможные операции неполного склеивания в два этапа:

а) проведём полное склеивание каждой из конституент единицы ДНФ (4) с последующими (полное склеивание – ).

1-й член склеивается со 2-м по , получим ,

1-й член склеивается с 5-м по , … ,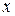

2-й член ни с чем не склеивается

3-й член склеивается с 4-м по , … ,

4-й член склеивается с 5-м по , … .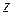

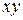б) конъюнкции, полученные в результате полного склеивания, выпишем в начале ДНФ, соединив между собой и с остальными членами ДНФ знаками дизъюнкции:

3. Проведём все возможные операции поглощения в соответствии с формулой .

Член поглощает и , т.е.

Аналогично, поглощает . Далее,

поглощает и 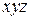. В итоге получим

(5)

– сокращённая ДНФ, (rang = 2).

4. Непосредственной проверкой убеждаемся, что дальнейшее применение операций склеивания и поглощения невозможно. Полученное соотношение (5) является сокращённой ДНФ заданной функции.

Конъюнктивные члены (5) представляют собой простые импликанты функции .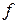

3.3.5. Построение минимальных ДНФ методом Петрика

Тупиковой ДНФ булевой функции называется дизъюнкция из некоторых простых импликант этой функции, равная самой функции и такая, что исключение из неё любой из импликант нарушает это равенство.

Произвольная булева функция может иметь несколько тупиковых форм. Те из них, которые имеют наименьшую сумму рангов, являются минимальными ДНФ. Следовательно, для отыскания минимальных ДНФ достаточно получить все её тупиковые формы и выбрать среди них минимальные.

В качестве универсального метода решения этой задачи приведём изложение метода Петрика.

Пусть совершенная ДНФ (СДНФ) функции f имеет k конституент, а её сокращённая ДНФ имеет m простых импликант.

1. Обозначим каждую простую импликанту f через p_i, т.е. имеем набор p₁,p₂, …, p_m.

2. Выделим те простые импликанты сокращённой ДНФ функции f, которые поглощают каждую из конституент единицы исходной ДНФ. Из простых импликант, поглощающих первую конституенту, образуем дизъюнкцию d₁; из простых импликант, поглощающих вторую конституенту, образуем дизъюнкцию d₂ и т.д. вплоть до k -ой конституенты. В итоге получим набор дизъюнкций d₁,d₂, …, d_k.

3. Из дизъюнкций d_i, полученных в п.2), образуем конъюнкцию

F(p₁,p₂,…,p_m) = d₁d₂…d_k (6)

4. Раскроем скобки в правой части (6) и проведём все возможные поглощения (в правой части (6) каждая из дизъюнкций d_i выражена через соответствующие импликанты p_i).

Обозначим число элементарных конъюнкций в полученном выражении через s. Каждой такой элементарной конъюнкции соответствует одна тупиковая форма функции f, которая получится, если в элементарной конъюнкции символы импликант p_i заменить их значениями, а знаки конъюнкций заменить знаками дизъюнкций. Т.о., получим s тупиковых ДНФ функции f. Для нахождения искомой минимальной ДНФ остаётся выбрать те из них, которые имеют наименьшую сумму рангов.

Пример 1: для булевой функции f из предыдущего примера построить тупиковые и минимальные ДНФ. Ранее была получена сокращённая ДНФ (10.5):

1. Выпишем её простые импликанты:

.

2. Выясним, каким импликантами поглощается каждая из конституент единицы исходной ДНФ (в которой все конъюнктивные члены приведены к одному рангу)

,

и образуем из них соответствующие дизъюнкции:

поглощается импликантами p₁, p₂; образуем d₁ = p₁ Ú p₂

поглощается импликантами p₁ ­_; образуем d₂ = p₁

поглощается импликантами p₃; образуем d₃ = p₃

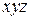поглощается импликантами p₃, p₄; образуем d₄ = p₃ Ú p₄

поглощается импликантами p₂, p₄; образуем d₅ = p₂ Ú p₄.

3. Из дизъюнкций d_i образуем конъюнкцию F

F = d₁d₂d₃d₄d₅ = (p₁ Ú p₂)p₁p₃(p₃ Ú p₄)(p₂ Ú p₄).

4. Раскроем скобки и, используя соотношение х* х = х, преобразуем:

F = (p₁p₁p₃ Ú p₂p₁p₃)(p₃p₂ Ú p₄p₂ Ú p₃p₄ Ú p₄p₄) = (p₁p₃ Ú p₁p₂p₃)(p₂p₃ Ú p₂p₄ Ú p₃p₄ Ú p₄).

В первых скобках p₁p₃ поглощает (p₁p₃)p₂, т.е. p₁p₃ Ú p₁p₂p₃ = p₁p₃. Во вторых скобках p₄ поглощает p₃p₄ и p₂p₄, тогда

p₄ Ú p₄p₃ Ú p₄p₂ = (p₄ Ú p₄p₃) Ú p₄p₂ = p₄ Ú p₄p₂ = p₄. После этих поглощений F принимает вид:

F = (p₁p₃)(p₂p₃ Ú p₄) = p₁p₃p₂p₃ Ú p₁p₃p₄ = p₁p₂p₃ Ú p₁p₃p₄.

Каждой элементарной конъюнкции в полученном выражении соответствует одна тупиковая форма ДНФ исходной f, для получения которой достаточно заменить импликанты рассматриваемой конъюнкции по п.1), соединив их знаками дизъюнкции. Т.о., имеем две тупиковые формы:

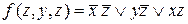, (årang = 6),

, (årang = 6).

Обе формы имеют одну и ту же сумму рангов, поэтому обе эти формы являются минимальными.

Замечание: задача о нахождении минимальной конъюнктивной формы булевой функции может быть сведена к нахождению минимальной ДНФ. Для этого достаточно:

1. Найти min ДНФ функции f.

2. Применить к ней операции отрицания и преобразовать по формулам Моргана.

3.3.6. Технические применения алгебры логики

Аппарат алгебры логики широко используется при описании работы т.н. контактных схем и цифровых машин. При проектировании таких схем на основе анализа условий работы схемы составляются логические функции, описывающие работу схемы.

При этом возникают два типа задач:

1. Для заданной схемы построить логическую функцию, работу этой схемы.

2. Построить схему, соответствующую данной логической функции.

Рассмотрим эти задачи, предварив их замечаниями.

Пусть высказывание 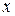= {контакт 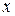замкнут}, тогда отрицание = {контакт замкнут} = {контакт 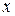не замкнут}. Рассмотрим участок схемы

- два последовательных контакта. Этот участок замкнут, если одновременно замкнуты 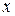и . В алгебре логики эта ситуация описывается конъюнкцией высказываний 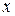и , т.е. .

– параллельные контакты. Здесь для замкнутого участка имеем дизъюнкцию.

Пример 1: для 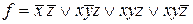построить соответствующие ей и её минимальным ДНФ контактные схемы.

Конъюнктивным членам заданной функции соответствуют участки схемы с последовательно расположенными на них контактами. А т.к.

конъюнктивные члены соединены между собой знаками дизъюнкции, то эти

Рис.1. Исходная контактная схема

участки подключены параллельно. Следовательно, схема имеет 11 контактов и изображается как на рис.1.

Для двух её минимальных ДНФ и контактные схемы будут иметь вид:

и содержат по шесть контактов.

Второй тип задачи.

Пример 2: составить логическую функцию, соответствующую контактной схеме:

;

.

Представление логической функции в виде графа.

На практике удобно изображать логическую функцию в виде дерева, где висячим вершинам соответствуют булевы переменные или их отрицания, а во внутренних вершинах размещены операции, которые нужно выполнить над переменными.

Пример 3: f(X,Y,Z) = XY Ú ØCUØZ Ú ØUØZ. Этой функции будет соответствовать граф:

Вопросы для самопроверки по теме 3.3

1. Дайте определения отрицания, конъюнкции, дизъюнкции, эквиваленции.

2. Напишите формулы Моргана.

3. Что называется булевой функцией?

4. Сколько различных булевых функций можно построить для функции ?

5. Что такое СДНФ, СКНФ?

6. Напишите соотношения полного и неполного склеивания, соотношение поглощения.

7. Что называется тупиковой ДНФ, минимальной ДНФ.

Заключение. Многие из рассматриваемых в настоящем курсе задач следует решать с привлечением табличного процессора Excel. Существенно проще делать их в математических пакетах, перечисленных во введении. Что касается задач на графах, решения обычных и дифференциальных уравнений, то, вообще говоря, применение этих средств является единственной альтернативой рутинным вычислениям «на бумаге». Поэтому следует, по возможности, овладевать навыками работы с этими современными и мощными инструментами. Желаем успехов!

Вопросы для подготовки к зачету Вы найдёте ниже (с.118).

Учебное пособие

Учебное пособие издано отдельным томом.