Совершенные нормальные формы

Определение 5. Совершенной дизъюнктивной нормальной формой формулы алгебры высказываний (СДНФ) называется ее ДНФ, обладающая следующими свойствами:

1. Она не содержит двух одинаковых слагаемых.

2. Ни одно слагаемое не содержит одновременно двух одинаковых сомножителей.

3. Ни одно слагаемое не содержит одновременно некоторого высказывания и его отрицания.

4. Каждое слагаемое содержит в качестве сомножителя либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.

Это определение является конструктивным, т.е. позволяет для каждой формулы алгебры высказываний, приведенной к ДНФ, построить ее СДНФ.

Упражнение 2.2.5

Задана ДНФ. Приведем ее к СДНФ.

1. Первое и последние слагаемые одинаковы. На основании свойства операции дизъюнкции АÚА=А одно из одинаковых слагаемых можно отбросить.

2. АСС=АС.

3. .

Получим .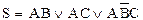

Теперь выполнили условия 1 – 3. Чтобы выполнить условие 4, поступим следующим образом:

;

Следовательно, .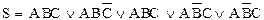

Теперь условие 4 выполнено, но появились одинаковые слагаемые. Исключив их, получим:

Определение 6. Совершенной конъюнктивной нормальной формой данной формулы алгебры высказываний (СКНФ) называется такая ее КНФ, которая удовлетворяет следующим свойствам:

1. Она не содержит двух одинаковых сомножителей.

2. Ни один из сомножителей не содержит одновременно двух одинаковых слагаемых.

3. Ни один из сомножителей не содержит одновременно некоторого высказывания и его отрицания.

4. Каждый сомножитель СКНФ содержит в качестве слагаемого либо переменное высказывание, либо его отрицание для всех переменных, входящих в формулу.

Определение СКНФ также является конструктивным.

Упражнение 2.2.6

Дана КНФ: .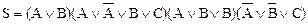

Построить СКНФ.

1. АÚВÚВ=АÚВ.

2. (АÚВ)(АÚВ)=АÚВ.

3. , следовательно, .

4. .

Следовательно, ,

Из определений и теорем 3, 4 следует, что тождественно истинная формула не имеет СКНФ, а тождественно ложная – СДНФ.

Каждая не тождественно истинная и не тождественно ложная формула имеет единственную СКНФ и СДНФ.

Совершенные нормальные формы могут быть применены для установления равносильности двух заданных формул алгебры высказываний. Для этого нужно обе формулы привести к СКНФ или СДНФ и убедить в их совпадении. Например, формулы

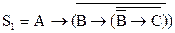и равносильны:

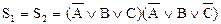Полной элементарной конъюнкцией называется конъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 5. Аналогично, полной элементарной суммой называется элементарная дизъюнкция, удовлетворяющая свойствам 2, 3, 4 определения 6.

Поэтому совершенные нормальные формы можно определить так:

Определение 7. Совершенной дизъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией различных полных элементарных конъюнкций.

Определение 8. Совершенной конъюнктивной нормальной формой некоторой формулы алгебры высказываний называется формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией различных полных элементарных дизъюнкций.

Каждая полная элементарная конъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 1: переменное высказывание, входящее без знака отрицания, принимает значение 1, а со знаком отрицания – 0. Этот набор значений элементарных составляющих называется единицей данной полной элементарной конъюнкции. Так, единицей полной элементарной конъюнкции является (1, 0,1).

Аналогично каждая полная элементарная дизъюнкция на одном наборе значений переменных высказываний, ее составляющих, обращается в 0: переменное высказывание, входящее без знака отрицания, принимает значение 0, а со знаком отрицания – 1. Этот набор значений элементарных составляющих называется нулем данной полной элементарной дизъюнкции. Так, нулем полной элементарной дизъюнкции является (1, 1,0).

Эти сведения непосредственно используются в следующем разделе данного учебного пособия.

Построение формулы алгебры высказываний
по заданной логической функции

Рассмотрим задачу, обратную той, о которой шла речь в разделах 2.1, 2.2 – построение функции для некоторой формулы алгебры высказываний. Задана некоторая функция f(x₁, x₂,... x_n), нужно построить для нее формулу S. Задача эта неоднозначна, существует множество равносильных между собой формул, соответствующих этой функции. Будем строить совершенную нормальную форму. При этом учтем, что полная элементарная дизъюнкция имеет единственный ноль, а полная элементарная конъюнкция – единственную единицу. Решение задачи рассмотрим на примере.

Таблица 2.3.1

x	y	z	f

Пусть задана некоторая функция трех аргументов f(1,1,1)=f(1,0,0)=f(0,1,0)=1. Это значит, что на наборах (1,1,1), (1,0,0), (0,1,0) функция принимает значение 1, а на остальных наборах – 0.

Построим S в виде совершенной дизъюнктивной нормальной формы. Так как S не тождественно ложна, это можно сделать. СДНФ состоит из стольких слагаемых, сколько единиц содержит функция. Первому значению 1 соответствует слагаемое xyz, принимающее значение 1 при х=1, y=1, z=1. Второму значению 1 соответствует слагаемое , принимающее значение 1 при х=1, y=0, z=0. Аналогично третье слагаемое, соответствующее 1, стоящей в шестой строке таблицы f, есть . Следовательно, . Итак:

1) Совершенная дизъюнктивная нормальная форма содержит столько слагаемых, сколько единиц имеет функция.

2) Эти единицы соответствуют тем наборам переменных, при которых каждое слагаемое (элементарная конъюнкция) обращается в единицу, т.е. переменным, входящим в элементарную конъюнкцию без знака отрицания, соответствует значение 1, а со знаком отрицания – 0.

Чтобы написать СКНФ по заданной функции, нужно выбрать все значения 0, встречающиеся в ней, и рассмотреть наборы значений переменных, отвечающие этим нулям. В заданном примере таблица содержит пять нулей. Первому значению 0 отвечает сомножитель 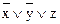, обращающийся в 0 при х=1, y=1, z=0. Второму – при х=1, y=0, z=1 и т.д. В результате получим

Итак:

1. СДНФ содержит столько сомножителей, сколько нулей имеет истинностная таблица.

2. Эти нули соответствуют тем наборам переменных, при которых каждый сомножитель (каждая элементарная сумма) обращается в 0, т.е. переменным, входящим в элементарную сумму без знака отрицания, соответствует значение 0, а со знаком отрицания – 1.

Заметим, что, используя список основных равносильных формул, полученные выражения для S упрощают, если это возможно.

Моделирование алгебры высказываний
с помощью релейно-контактных схем

Релейно-контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакты могут быть размыкающими и замыкающими. Каждый контакт подключен к некоторому реле. Когда реле находится под током, все подключенные к нему замыкающие контакты замкнуты, а размыкающие – разомкнуты.

Каждому реле можно поставить в соответствие значение 1, если оно находится под током, и 0, если нет. Все замыкающие контакты, подключенные к реле х, будем обозначать x₁,... x_n, а размыкающие – .

Всей схеме также можно поставить одно из двух значений 1, если схема проводит ток, и 0, если не проводит. Это значение есть функция переменных х_i, , т.е. логическая функция. Эту функцию называют функцией проводимости электрической цепи.

Всякая формула алгебры высказываний может быть реализована некоторой релейно-контактной схемой, имеющей соответствующую функцию проводимости. И наоборот, для некоторой схемы можно указать ее функцию проводимости, логическую функцию, а затем построить для нее некоторую формулу алгебры высказываний. При этом основные логические связки моделируются следующими элементарными схемами:

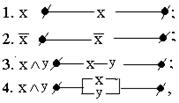
т.е. дизъюнкция моделируется параллельным соединением проводников, конъюнкция – последовательным.

Упражнение 2.3.1

Построить функцию проводимости следующей схемы:

Рис. 2.3.1

Функция проводимости для такой схемы задается, очевидно, следующей таблицей:

Таблица 2.3.2

x	y	z	f(x,y,z)

По данной логической функции построим формулу – СКНФ:

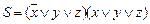
Упростим это выражение: .

Построим более простую схему, имеющую ту же функцию проводимости, что и исходная:

Y Z

Рис. 2.3.2

Чтобы упростить релейно-контактную схему, не обязательно строить ее функцию проводимости. Можно написать соответствующую данной схеме формулу и упростить. Затем построить схему электрической цепи, моделирующую эту упрощенную формулу. Так, для электрической цепи, приведенной в данном примере, .