Будем пользоваться следующими символами A, B, C,..., X, Y, Z...
– переменные высказывания, 0, 1, И, Л – const, Ù, Ú, ®, «,
– символы соответствующих логических операций.
Дадим определение формулы алгебры высказываний:
1) отдельно стоящая буква A, B, C,..., X, Y, Z... – формула.
2) если А, В – формулы, то формулами являются и (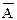 ), (
), (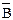 ), (АÙВ), (АÚВ), (А®В), (А«В).
), (АÙВ), (АÚВ), (А®В), (А«В).
3) Других формул нет.
Очевидно, сложное высказывание выше приведенного примера задано формулой S.
Две формулы алгебры высказываний называются равносильными, если на всех одинаковых наборах значений составляющих переменных высказываний они принимают одинаковые значения 1 или 0.
Упражнение 2.1.2
Следующие высказывания могут быть интерпретированы как составные. Указать элементарные высказывания их составляющие, написать формулы данных высказываний и построить истинностные таблицы. Указать, какие из высказываний равносильны.
S1: Х неверно сделал расчет или если Y считал задачу правильно, то и Z сделал это без ошибок.
S2: Если Х правильно просчитал задачу, то либо Y ошибся, либо Z сделал ее верно.
S3: Либо Х неверно просчитал задачу, либо Y решил ее верно в том и только в том случае, если Z решил ее верно.
Очевидно, данные сложные высказывания составлены из следующих элементарных.
А: Х правильно просчитал задачу
B: Y правильно просчитал задачу
C: Z правильно просчитал задачу
Используя основные логические связки, запишем формулы данных высказываний.
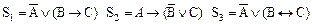
Составим истинностные таблицы данных высказываний:
Таблица 2.18
| А | В | С | В®С | S1 | 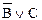 | S2 | В«С | S3 |
Из таблицы 2.1.8 видно, что высказывания S1 и S2 равносильны: S1=S2.
Приведем список основных равносильных формул алгебры высказываний:
| АÚА=А |
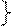 | |||
| АÙА=А | ||||
| АÚВ=ВÚА |
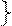 | |||
| АÙВ=ВÙА | ||||
| (АÚВ)ÚС=АÚ(ВÚС) |
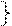 | |||
| (АÙВ) ÙС=АÙ (ВÙС) | ||||
| АÙ (ВÚС)=(АÙВ) Ú(АÙС) |
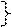 | |||
| АÚ (ВÙС)=(АÚВ) Ù(АÚС) | ||||
| AÚИ=И | ||||
| AÙЛ=Л | ||||
| AÙИ=A | ||||
| AÚЛ=A | ||||
AÚ 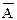 =И =И | закон исключенного третьего | |||
AÙ 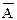 =Л =Л | ||||
 | ||||
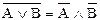 |
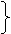 | |||
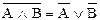 | ||||
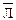 =И =И | ||||
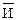 =Л =Л |
Отметим, что операции импликации и двойной импликации можно заменить дизъюнкцией, конъюнкцией, отрицанием, используя следующие равносильные формулы:
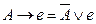 ,
,
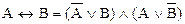 ,
,
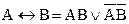 .
.
Рассмотрим множество всех логически возможных случаев, множество всех возможных логических ситуаций для высказываний, связанных с некоторой проблемой, – некоторое универсальное множество. Поставим в соответствие каждому переменному высказыванию некоторое подмножество универсального множества логических возможностей и назовем его множеством истинности данного высказывания. Множество истинности данного высказывания содержит в качестве своих элементов все те логически возможные случаи, когда данное высказывание является истинным.
Высказыванию, истинному во всех логически возможных случаях, т.е. логической константе, обозначаемой 1 или И, будет соответствовать универсальное множество. Высказыванию, ложному во всех логически возможных случаях, т.е. логической константе, обозначаемой 0 или Л, будет соответствовать пустое множество. Тогда дизъюнкции двух высказываний будет соответствовать объединение (сумма) их множеств истинности, конъюнкции – пересечение их множеств истинности, а отрицанию к высказыванию – дополнение к множеству истинности данного высказывания. Учитывая это и сравнивая список основных равносильных формул алгебры высказываний со списком свойств основных операций над множествами, убеждаемся в том, что операции алгебры высказываний образуют Булеву алгебру.
Заметим следующее: для того, чтобы убедиться в равносильности двух формул, можно построить их истинностные таблицы и убедиться в их совпадении. Равносильность формул можно установить также, убедившись в совпадении множеств истинности рассматриваемых высказываний. Так, в справедливости закона дистрибутивности №7 можно убедиться, изобразив на диаграммах Эйлера-Венна множества истинности левой и правой частей равенства (рис. 2.1.1).
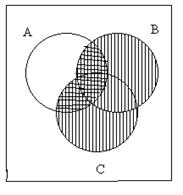
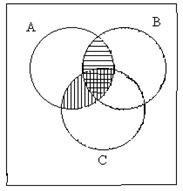
 |
.
Рис. 2.1.1
Установить равносильность формул можно также путем их преобразования. Так, заменяя импликацию равносильной ей формулой, получим равносильность формул S1 и S2 упражнения 2.1.2:
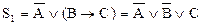 .
.
Рассмотрим некоторые упражнения на данную тему.
Упражнение 2.1.3
Указать множество наборов, удовлетворяющих уравнению
S=(xy®yz) Ú x Ú y Ú z=0.
Решение получим, построив истинностную таблицу данной формулы. Убеждаемся в том, что на всех 8 ми наборах истинности и ложности данных высказываний x, y, z формула принимает значение 1, т.е. наборов, где бы S принимала значение 0 нет, формула Sº1, т.е. тождественно истинна, т.е. наборов где бы S=0 нет.
К тому же результату можно прийти, преобразовав S и используя список основных равносильных формул:
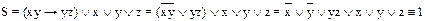 ,
,
т.к. а) 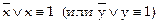 ,
,
б) 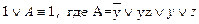 .
.
Упражнение 2.1.4
Проверить равносильность двух формул 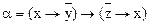 и
и 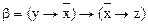 .
.
Преобразуем формулы, заменив импликацию равносильной формулой.
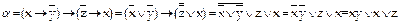 ,
, 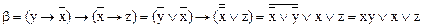 .
.
Очевидно, a=b.
Упражнение 2.1.5
При составлении расписания на понедельник преподаватели просили, чтобы уроки проходили в следующем порядке:
1) математика первым или третьим уроком;
2) история – первым или вторым;
3) литература – вторым или третьим.
Можно ли удовлетворить просьбы всех трех преподавателей и, если это возможно, то каким образом?
Введем следующие элементарные высказывания:
А – математика – I ый урок
В – математика – III ий урок
С – история – II ой урок
D – история – I ый урок
E – литература – II ой урок
F – литература – III ий урок
Просьбы всех преподавателей выражены высказываниями S1=АÚВ, S2=CÚD, S3=EÚD.
Высказывание, удовлетворяющее просьбы всех трех преподавателей, очевидно, есть конъюнкция S1, S2, S3, т.е. S = S1 Ù S2 Ù S3, и оно должно быть истинным, т.е. S=1. Применим дистрибутивный закон №7 в преобразованиях S:
S=(AÚB)(CÚD)(EÚF)=(ACÚBCÚADÚBD)(EÚF).
В данном случае конъюнкция AD=0, т.к. первым уроком математика и история одновременно быть не могут.
S=ACЕÚBCЕÚBDЕÚACFÚBCFÚBDF.
Очевидно, АСЕ=0, т.к. СЕ=0: второй урок не может быть одновременно уроком истории и литературы. Аналогично: ВСЕ=0, BCF=0, BDF=0, т.е. S= BDЕÚACF=1.
Дизъюнкция истинна, если одно из слагаемых истинно: BDЕ=1; ACF=1.
Конъюнкция высказываний истинна, если истинны все входящие в нее сомножители. В результате получаем два возможных варианта ответа:
1) BDЕ=1, т.е. история – I ый урок,
литература – II ой урок,
математика – III ий урок.
2) ACF=1, т.е. математика – I ый урок
история – II ой урок,
литература – III ий урок.
Варианты импликации
В математике весьма важными являются понятия: «необходимое условие», «достаточное условие», которые могут быть записаны с помощью связи импликации.
«А достаточное условие для В», очевидно выражается формулой: А®В, а «А необходимое условие для В» – формулой В®А, которую называют конверсией импликации. В конверсии импликации посылка А и заключение В меняются местами.
Достаточное условие может быть выражено формулой, равносильной формуле А®В, а именно 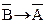 , называемой контроппозицией, а необходимое условие – формулой
, называемой контроппозицией, а необходимое условие – формулой 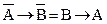 , называемой конверсией контроппозиции.
, называемой конверсией контроппозиции.
В рассуждениях эти равносильные формулы заменяют друг друга. Кроме того, «А достаточно для В» может быть выражено в виде «А только, если В», (не путать с «А если и только если В»), т.к. это означает: «Если не В, то не А», т.е.
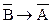 =А®В.
=А®В.
Итак, получим:
«А достаточно для В»: А®В= 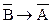 , «А только, если В»;
, «А только, если В»;
«А необходимо для В»: 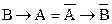 .
.
Очевидно, необходимое и достаточное условие выражается двойной импликацией 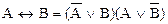
Упражнение 2.1.6
Написать формулы следующих высказываний.
S1: дифференцируемая функция непрерывна;
S2: функция дифференцируема только в случае ее непрерывности;
S3: функция непрерывна только в случае ее дифференцируемости;
S4: дифференцируемость функции есть необходимое условие ее непрерывности;
S5: дифференцируемость функции есть достаточное условие ее непрерывности;
S6: дифференцируемость функции есть необходимое и достаточное условие ее непрерывности.
Введем в качестве элементарных имен высказывания: А – данная функция дифференцируема, В – данная функция непрерывна.
Очевидно: S1=А®В; S2: «А только, если В», т.е. «Если 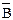 , то
, то 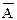 «, т.е.
«, т.е. 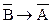 =А®В; S3: «В только, если А», т.е.
=А®В; S3: «В только, если А», т.е. 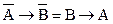 ; S4=В®А; S5=А®В; S6=А«В.
; S4=В®А; S5=А®В; S6=А«В.
Итак, высказывания S1, S2, S5 выражают достаточность А для В, а высказывания S3, S4 – необходимость.
 2015-10-22
2015-10-22 2475
2475
