Отсутствием какого из свойств отношений отличаются отношение толерантности от отношения эквивалентности?

а) рефлексивности;

б) симметрии;

в) транзитивности.

Тема 2.

Математическая логика

Математическая логика представляет собой формальный математический аппарат, изучающий различные способы логических рассуждений.

Алгебра высказываний

Простейшую из формальных логических теорий называют алгеброй высказываний. Из высказываний состоит любое логическое рассуждение. Высказывание – предложение, относительно которого можно утверждать, истинно оно или ложно. Так, предложение «5>1», «13 делится на 5» – высказывания. Но «Который час?», «Да здравствует математика!» – не являются высказываниями в связи с данным определением. Если высказывание истинно (ложно) в любой логической ситуации, то оно называется тождественно истинным (ложным), или логической константой, обозначаемой соответственно И(Л). Высказывания, истинные в одних логических ситуациях и ложные в других, называются переменными высказываниями. Все приведенные выше высказывания представляют собой так называемые элементарные высказывания.

Логические операции

Обозначим элементарные высказывания латинскими буквами A, B, C,..., X, Y, Z...

Конъюнкция. Обозначается АÙВ (А&В, АВ), читается: А и В. Получили сложное высказывание, составленное из двух элементарных. Значение истинности или ложности высказывания, являющегося конъюнкцией двух элементарных высказываний А и В, задается следующей истинностной таблицей:

Таблица 2.1.1

Все рассматриваемые в дальнейшем логические связи будут задавать с помощью аналогичных истинностных таблиц.

Чаще пользуются более удобным обозначением: «И» – 1, «Л» – 0. В этих обозначениях истинностная таблица конъюнкции будет иметь вид

Таблица 2.1.2

Итак, конъюнкция двух элементарных высказываний истинна тогда и только тогда, когда оба элементарных высказывания истинны.

Дизъюнкция. Обозначается АÚВ, читается: А или В. При этом разделительный смысл союза «или» исключается. Истинностная таблица дизъюнкции имеет вид:

Таблица 2.1.3

Дизъюнкция двух элементарных высказываний является ложным высказыванием тогда и только тогда, когда оба высказывания, ее составляющие, ложны.

Отрицание. Единственная логическая операция, относящаяся к одному высказыванию, – унарная, в отличие от остальных – бинарных. Обозначается: 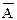(>А, ~А), читается: не А. Истинностная таблица имеет вид:

Таблица 2.1.4

Импликация. Обозначается А®В (АÌВ), читается: если А, то В. При этом А называют посылкой, В – следствием. Импликация задается следующей истинностной таблицей:

Таблица 2.1.5

Импликация ложна тогда и только тогда, когда посылка А истинна, а следствие В – ложь.

Двойная импликация. Обозначается А«В (А~В), читается: А тогда и только тогда, когда В. Задается следующей истинностной таблицей:

Таблица 2.1.6

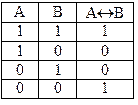
Двойная импликация является истинностным высказыванием тогда и только тогда, когда высказывания А и В, ее составляющие, принимают одинаковое значение истинности или ложности.

Приведем пример. Пусть А и В – элементарные высказывания: А – «Этот четырехугольник – параллелограмм», В – «Этот четырехугольник – ромб». Образуем из этих двух элементарных высказываний сложные, используя перечисленные логические связки.

Сложное высказывание АÙВ, очевидно, читается так: «Этот четырехугольник есть параллелограмм и ромб». Значения истинности и ложности этого высказывания определяется таблицей 2.1.2. Это высказывание считают истинным в том и только в том случае, когда оба высказывания А и В – истинны.

Дизъюнкция указанных высказываний АÚВ читается: «Этот четырехугольник есть параллелограмм или ромб». Значение истинности и ложности этого высказывания определяется таблицей 2.1.3. Очевидно, для импликации и двойной импликации получим соответственно А®В: «Если этот четырехугольник есть параллелограмм, то он – ромб»; А«В «Этот четырехугольник есть параллелограмм тогда и только тогда, когда он – ромб». Значение истинности или ложности этих высказываний определяется таблицами 2.1.5 и 2.1.6. Отрицание к А, т.е. 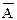, есть высказывание: «Неверно, что этот четырехугольник есть параллелограмм» или «Этот четырехугольник не параллелограмм».

Пользуясь указанными логическими связками, их истинностными таблицами, можно построить сколь угодно сложное высказывание и найти его истинностную таблицу.

Заметим, что число строк истинностной таблицы, очевидно, равно , где n – число элементарных высказываний.

Упражнение 2.1.1

Построим истинностную таблицу сложного высказывания:

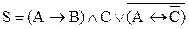
Очевидно, истинностная таблица будет содержать строк. Скобки применяются, если нарушаются естественный порядок операций: отрицание, конъюнкция, дизъюнкция, импликация, двойная импликация. Скобки (А®В) указывают на то, что сначала нужно выполнить импликацию, затем найти (А®В)ÙС. Скобки в выражении 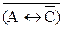можно опустить. Заключительной операцией в построении истинностной таблицы для S будет дизъюнкция двух высказываний: (А®В)ÙС и .

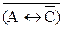Таблица 2.1.7

А	В	С	А®В	(А®В)ÙС

Итак, формула S задает высказывание, которое истинно на следующих наборах значений элементарных высказываний:

А=1	В=1	С=1	(все три элементарных высказывания истинны)
А=1	В=0	С=1	(А, С – истинны, В – ложно)
А=0	В=1	С=1	(А – ложно, В и С – истинны)
А=0	В=1	С=0	(В – истинно, А и С – ложны)
А=0	В=0	С=1	(С – истинно, А и В – ложно)
А=0	В=0	С=0	(все три высказывания ложны).