2017-10-25
710
При выводе формул зависимости координат точки местности и снимка необходимо определить соотношения между камерой/сенсором, снимком и земной поверхностью.
Большинство фотограмметрических задач используют следующие формулы в том или ином виде:
, (1)
где 
– пространственные фотограмметрические координаты точки 
снимка;
– элементы внутреннего ориентирования снимка;
– плоские прямоугольные координаты точки на снимке;
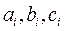– значения направляющих косинусов углов луча визирования на точку М на местности;
– фокусное расстояние камеры прибора.
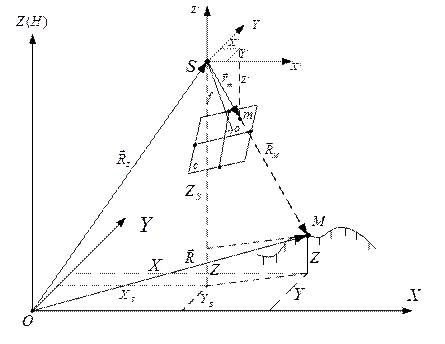
Рисунок 1 – Зависимость между координатами
точки местности и снимка
(2)
Из рисунка 1 видно, что вектор 
на снимке может быть определен как вектор, проведенный из точки фотографирования 
в точку снимка 
. Вектор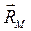 
на поверхности земли или объекта может быть определен как вектор, проведенный из точки фотографирования 
в точку на поверхности М. Вектора на изображении 
и на поверхности 
коллинеарны если один из них является скалярным кратным по отношению к другому. Это логически вытекает из того, что линия, проходящая через точку фотографирования и точку на снимке или поверхности, является прямой.
Предположим, что даны пространственные фотограмметрические координаты точки снимка 
. Необходимо найти пространственные координаты точки на местности.
. (3)
– координаты точки 
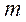в системе координат 
; 
;
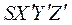. (4)
. (5)
,
. (6)
,
. (7)
,
,
. (8)
Формулы – строгие, точные и пригодные для любых снимков с точностными параметрами. В представленных формулах в двух уравнениях имеются три неизвестных (
). Координату 
можно не учитывать при обработке снимков на плоские и всхолмленные районы. Однако, один снимок позволяет составить для каждой изобразившейся на нем точке два уравнения с тремя неизвестными координатами (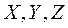
), а этого недостаточно для определения пространственного положения объекта на местности.
