Уравнение плоскости, проходящей через три различные точки 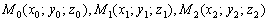 , которые не лежат на одной прямой, можно составить по формуле:
, которые не лежат на одной прямой, можно составить по формуле:
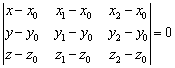
На самом деле это разновидность предыдущего способа, смотрим на картинку:
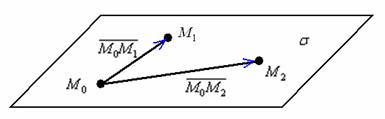
Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных данной плоскости:
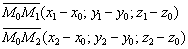
Пример
Составить уравнение плоскости по точкам 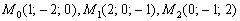 .
.
Решение: составим уравнение плоскости по трём точкам. Используем формулу:
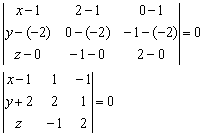
Раскрываем определитель по первому столбцу, находим уравнение плоскости:
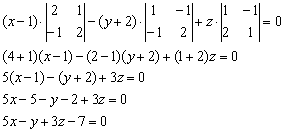
Больше ничего упростить нельзя, записываем:
Ответ: 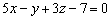
Пример
Уравнение плоскости
в отрезках
Преобразуем полное общее уравнение плоскости:
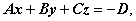
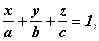
Где 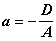 ,
, 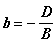 и
и 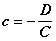 будут отрезки, отсекаемые плоскостью на осях координат.
будут отрезки, отсекаемые плоскостью на осях координат.

Рис.
Построить плоскость 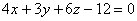
Решение: сначала составим уравнение плоскости в отрезках. Перебросим свободный член направо и разделим обе части на 12:
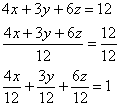
Делаем дроби трёхэтажными:
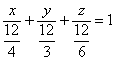
Именно так! – ведь знаменатели могут оказаться и дробными. Но в данном случае всё разделилось нацело:
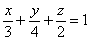
Таким образом, плоскость проходит через точки 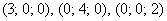 . В целях самоконтроля координаты каждой точки устно подставим в исходное уравнение
. В целях самоконтроля координаты каждой точки устно подставим в исходное уравнение 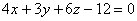 . После чего выполним чертёж:
. После чего выполним чертёж:
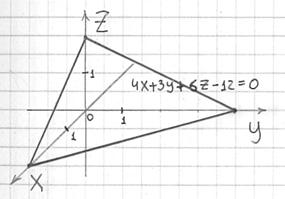
Задача 6.
Приведенная ниже формула площади используется в задачах когда вершины треугольника заданы на плоскости координатами 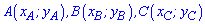 . В этом случае площадь равна половине определителя взятого по модулю.
. В этом случае площадь равна половине определителя взятого по модулю.
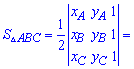
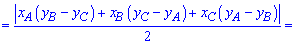
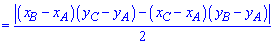
Найти площадь пятиугольника, изображенного на рисунке. 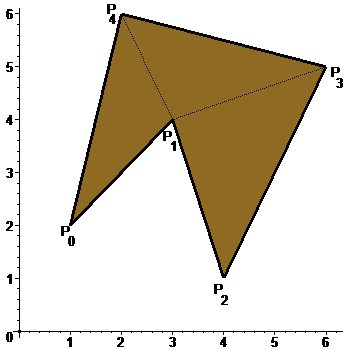
Решение. Имеем: 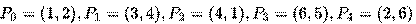 .
.
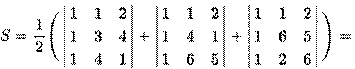
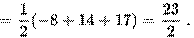
 2017-11-30
2017-11-30 587
587







