Теоретические вопросы к разделу 5

Экстремум функции, его классификация

Необходимое условие экстремума в точке :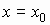

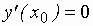, или 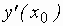, – не существует.

При этом если 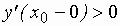; 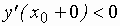– в точке 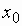функция имеет максимум;

Если 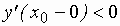; 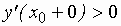– минимум.

Если производная свой знак не меняет, то экстремума нет, точка 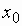– называется критической или стационарной.

Пример 1. Исследовать на экстремум:

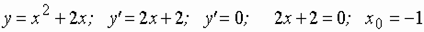– критическая точка.

Находим знак производной слева и справа от точки .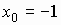

 

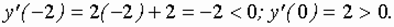т.е.

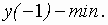
Пример 2. Исследовать на экстремум:

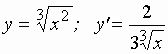– не существует в точке .

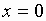Находим знак производной в окрестности критической точки:

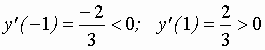, т.е. .

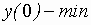Пример 3. Исследовать на экстремум:

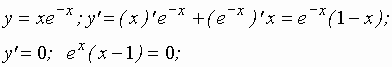
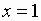– критическая точка.

Находим знаки производной в окрестности критической точки :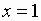

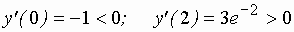т.е. .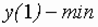

Теоретические вопросы к разделу 4

1. Необходимые условия экстремума.

2. Достаточные условия экстремума.

Задание к разделу 4. Исследовать на экстремум:

 

 

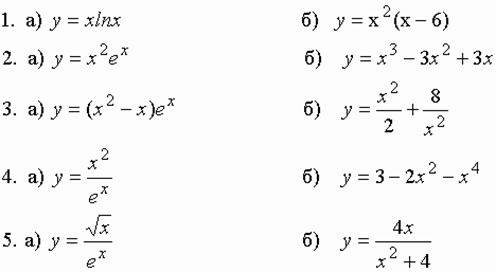
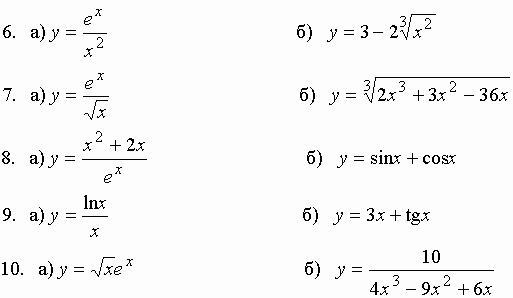
Раздел 5. Наибольшее и наименьшее значение

функции 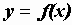на отрезке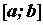

Задача нахождения наибольшего и наименьшего значения функции на отрезке решается в такой последовательности:

• находятся критические точки функции и отбираются те, которые попали в заданный интервал;
• находится значение функций в этих точках и на границе интервала.

Из полученных значений выбираются наибольшие и наименьшие значения.

Пример 1

Найти наибольшее и наименьшее значение функции 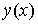на интервале :

.

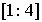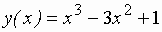Решение:

• находим критические точки:

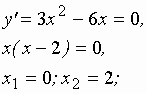
в интервал [1;4] попадает только .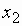

• Находим значение функции в точке

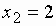
и на границах интервала:

; ; ,

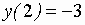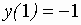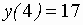т.е. наибольшее значение функции 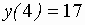, наименьшее – .

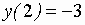Теоретические вопросы к разделу 5

1. Условия существования критической точки.

2. Определение наибольшего и наименьшего значения функции на отрезке.