1. Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь и считать, что вся масса тела сосредоточена в одной геометрической точке. Положение материальной точки в пространстве задается радиус-вектором
 = x
= x  + y
+ y  + z
+ z  ,
,
где x, y, z – координаты точки;  ,
, 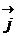 ,
,  – единичные векторы (орты).
– единичные векторы (орты).
Движение материальной точки в пространстве описывается одним векторным уравнением  = f (t) или эквивалентными ему тремя скалярными: x = f (t);
= f (t) или эквивалентными ему тремя скалярными: x = f (t);  = f (t);
= f (t);  f (t), где t – время.
f (t), где t – время.
2. Мгновенная скорость материальной точки
 ,
,
где  ;
;  ;
;  – проекции вектора скорости на оси координат.
– проекции вектора скорости на оси координат.
Модуль мгновенной скорости равен первой производной пути S по времени t
υ =  или
или 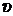 =
=  .
.
3. Средняя скорость
<  > =
> =  ,
,
где  – перемещение материальной точки за промежуток времени
– перемещение материальной точки за промежуток времени  t.
t.
4. Средняя путевая скорость
< υ > =  ,
,
где  – путь, который проходит материальная точка за промежуток времени
– путь, который проходит материальная точка за промежуток времени  .
.
5. Мгновенное (полное) ускорение материальной точки
 =
=  =
=  ,
,
где  ;
;  ;
;  – проекции вектора ускорения на оси координат.
– проекции вектора ускорения на оси координат.
Модуль мгновенного ускорения
|
|
|
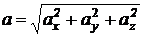 .
.
Полное ускорение можно представить как геометрическую сумму тангенциальной  и нормальной
и нормальной  составляющих
составляющих
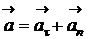
или в скалярной форме
 .
.
Числовые значения тангенциальной и нормальной составляющих ускорения
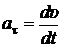 ;
;  ,
,
где R – радиус кривизны траектории в данной точке.
6. Кинематическое уравнение равномерного движения материальной точки относительно оси x
 ,
,
где  – координата материальной точки в момент времени t; x 0 – начальная координата (координата в момент времени t = 0);
– координата материальной точки в момент времени t; x 0 – начальная координата (координата в момент времени t = 0); 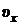 – проекция вектора скорости на ось x.
– проекция вектора скорости на ось x.
При равномерном движении 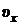 = const,
= const,  .
.
7. Кинематическое уравнение равнопеременного движения относительно оси x
 ,
,
где  – проекция вектора скорости на ось x в момент времени t = 0;
– проекция вектора скорости на ось x в момент времени t = 0;  – проекция вектора ускорения на ось x.
– проекция вектора ускорения на ось x.
При равнопеременном движении 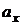 = const и скорость точки определяется уравнением
= const и скорость точки определяется уравнением
 .
.
8. Кинематическое уравнение вращательного движения материальной точки (или абсолютно твердого тела) относительно заданной оси вращения
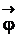 =
=  ,
,
где 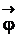 – угол поворота;
– угол поворота;  – время.
– время.
9. Угловая скорость  при вращательном движении определяется как первая производная угла поворота
при вращательном движении определяется как первая производная угла поворота  по времени t
по времени t
 .
.
Средняя угловая скорость
<  > =
> =  ,
,
где 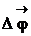 – приращение угла поворота за промежуток времени
– приращение угла поворота за промежуток времени  .
.
10. Угловое ускорение  равно первой производной угловой скорости по времени t
равно первой производной угловой скорости по времени t
 .
.
11. Кинематическое уравнение равномерного вращения относительно оси z
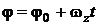 ,
,
где  – угол поворота в момент времени t;
– угол поворота в момент времени t;  – начальное значение угла поворота (угол поворота в момент времени t = 0);
– начальное значение угла поворота (угол поворота в момент времени t = 0);  – проекция вектора угловой скорости на ось z.
– проекция вектора угловой скорости на ось z.
При равномерном вращении  = const,
= const,  = 0.
= 0.
Равномерное вращательное движение характеризуется периодом вращения Т, то есть промежутком времени, за которое точка (тело) совершает один полный оборот:
|
|
|
 .
.
Количество оборотов, совершаемых точкой (телом) при равномерном вращении в единицу времени, называют частотой вращения
 .
.
12. Кинематическое уравнение равнопеременного движения относительно оси z
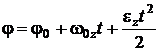 ,
,
где  – проекция вектора угловой скорости на ось z в момент времени
– проекция вектора угловой скорости на ось z в момент времени
t = 0;  – проекция вектора углового ускорения на ось z.
– проекция вектора углового ускорения на ось z.
При равнопеременном вращении 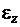 = const и угловая скорость точки (тела) определяется уравнением
= const и угловая скорость точки (тела) определяется уравнением
 .
.
13. Связь между линейными и угловыми величинами выражается формулами:
 ;
;  ;
;  ,
,
где R – радиус кривизны траектории в данной точке.
14. Среднее значение функции  за промежуток времени от t 1 до t 2определяется выражением
за промежуток времени от t 1 до t 2определяется выражением
< у > =  .
.
Пример 1. Точка движется по прямой согласно уравнению  . Определить среднюю путевую скорость < υ > точки в интервале времени от t 1= 2 c до t 2 = 6 c.
. Определить среднюю путевую скорость < υ > точки в интервале времени от t 1= 2 c до t 2 = 6 c.
Дано: 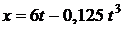 ;
; 
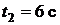 .
.
Найти: < υ >.
Решение. Найдем координаты точки в моменты времени t 1 и t 2:
 ;
;
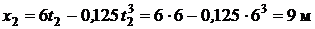 .
.
Проекция вектора скорости на ось x изменяется с течением времени по закону
 .
.
Найдем значения  в моменты времени t 1 и t 2:
в моменты времени t 1 и t 2:
 м/с;
м/с;
 м/с.
м/с.
Полученные результаты свидетельствуют о том, что направление движения точки изменяется на противоположное, так как в момент времени t 1 = 2 c точка движется в сторону положительного направления оси x (положительное значение 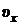 ), а в момент времени t 2 – в противоположном направлении (отрицательное значение
), а в момент времени t 2 – в противоположном направлении (отрицательное значение  ). Момент времени t 0, когда точка изменяет направление движения, найдем из условия
). Момент времени t 0, когда точка изменяет направление движения, найдем из условия 
 .
.
Тогда
 .
.
Отрицательное значение корня не удовлетворяет условию задачи, поэтому принимаем t 0 = 4 c.
Найдем координату точки в момент времени t 0:
 .
.
Найдем среднюю путевую скорость
< υ >  .
.
Произведем вычисления
< υ >  м/с.
м/с.
Ответ: < υ >=3 м/с.
Пример 2. Точка движется по дуге окружности радиуса R. Ее скорость зависит от пройденного пути S по закону 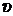
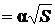 , где
, где  – постоянная. Найти угол
– постоянная. Найти угол  между вектором полного ускорения и вектором скорости в зависимости от S.
между вектором полного ускорения и вектором скорости в зависимости от S.
 Дано: R – радиус окружности, по которой движется точка;
Дано: R – радиус окружности, по которой движется точка;  − зависимость скорости от пройденного пути;
− зависимость скорости от пройденного пути;  – постоянная.
– постоянная.
Найти:  = f (S).
= f (S).
Решение: Из рисунка 1 видно, что

 , (1)
, (1)
где 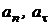 – нормальная и тангенциальная составляющие ускоре-
– нормальная и тангенциальная составляющие ускоре-
Рис.1 ния.
Нормальная составляющая ускорения равна  .
.
Тангенциальная составляющая ускорения

Подставляя значения  и
и  в уравнение (1), получим
в уравнение (1), получим  .
.
Анализ размерности показывает, что  величина безразмерная, и убеждает в правдоподобности ответа.
величина безразмерная, и убеждает в правдоподобности ответа.
Ответ:  .
.
Пример 3. Вентилятор вращается с частотой  об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 оборотов. Какое время t прошло с момента выключения до полной его остановки?
об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 оборотов. Какое время t прошло с момента выключения до полной его остановки?
Дано:  ; N = 75.
; N = 75.
Найти: t.
Решение: Пусть вентилятор вращается относительно оси z (рис. 2). Так как движение является равнозамедленным, то вектор углового ускорения  направлен противоположно вектору угловой скорости
направлен противоположно вектору угловой скорости  . Запишем уравнение движения относительно оси z
. Запишем уравнение движения относительно оси z
 (1)
(1)
|
|
 Проекция вектора угловой скорости на ось z изменяется с течением времени по закону
Проекция вектора угловой скорости на ось z изменяется с течением времени по закону  .
.
В момент остановки  , поэтому
, поэтому
 ,
,
|
Подставим это выражение в уравнение (1), учитывая, что 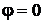 :
:
 .
.
|
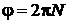 ;
;  , то
, то  .
.
Выполним проверку размерности
 .
.
Произведем вычисления
 .
.
Ответ: t = 10 c.
 2017-11-30
2017-11-30 1005
1005


