Пересекаются плоскости, у которых следы на одной плоскости проекций в пределах чертежа не пересекаются

На рисунке 46 заданы две плоскости Р и Q общего положения, у которых фронтальные следы в пределах чертежа не пересекаются.

Рис. 46 Рис. 47

Одна общая для этих плоскостей точка определяется на пересечении их горизонтальных следов (рис. 46).

Для нахождения второй точки линии пересечения заданных плоскостей Р и Q рассечем их вспомогательной третьей плоскостью R, параллельной плоскости проекции H (рис. 47). На рисунке 48 показано построение линий пересечения плоскости R с плоскостями Р и Q: плоскость R пересекает обе эти плоскости по горизонталям.

Рис. 48 Рис. 49

Построенные горизонтальные проекции этих двух горизонталей пересекаются в точке 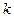(т.к. лежат в одной горизонтальной плоскости R); по линии проекционной связи вверх строим её фронтальную проекцию (рис. 49). Эта построенная точка является общей для всех трех плоскостей (рис. 49).

Рис. 50

Точка , являясь второй точкой, общей для заданных плоскостей Р и Q, вместе с ранее построенной точкой определяют линию пересечения этих плоскостей Р и Q (см. рис. 50).

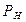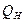На рисунке 50.1. показано решение подобной же задачи не вводя третьей секущей вспомогательной плоскости уровня (плоскости–паразита). В этом случае точка пересечения горизонтальных следов и плоскостей расположена во втором углу пространства. Пересечение заданных плоскостей Р и Q определяется линией .