2017-10-25
326
1. Раскрытие неопределённости 
. Надо числитель и знаменатель дроби разделить на высшую степень переменной.
Пример 1. Вычислите 
.3
Решение. Разделим каждое слагаемое числителя и знаменателя на х2. Получим:
= 
= 
=∞.
Ответ: = 
.
2. Раскрытие неопределённости 
.
1) Если под знаком предела стоит отношение двух многочленов 
и 
, то имеем неопределенность вида . В этом случае предел 
можно вычислить разложением многочленов 
и 
на множители, используя формулы сокращенного умножения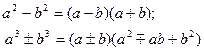 
или формулу разложения квадратного трехчлена на множители:
, где х 1 и х 2 – корни уравнения 
.
Если разложение выполнено верно, то в числителе и знаменателе дроби должны получиться одинаковые множители, которые следует сократить. После сокращения предел вычисляется простой подстановкой.
Пример 2. Вычислите 
.
Решение. Проверим, какие значения будут принимать числитель и знаменатель при подстановке вместо х значения 3: 
, 
.
Получили неопределенность вида .
Разложим числитель на множители по формуле разложения квадратного трехчлена. Составим уравнение 
и найдем его корни:
|
|
|
D = 
;
; 
3 или 
; 
.
Тогда числитель можно представить в виде произведения двух множителей: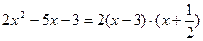 
= 
Знаменатель 
разложим по формуле разности квадратов: = 
.
Вернемся к исходному пределу:
= 
= 
.
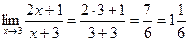Ответ: = 
.
2) Если под знаком предела стоит дробь вида 
, включающая иррациональную функцию (функцию, содержащую корень), то домножаем числитель и знаменатель дроби на выражение, сопряженное иррациональному.
Пример 3. Вычислите 
.
Решение. Поскольку при подстановке в числитель и знаменатель вместо х значение 0, получаем неопределенность вида , домножим числитель и знаменатель дроби на выражение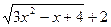 
, сопряженное знаменателю. Получим:
= 
.
В знаменателе дроби воспользуемся формулой разности квадратов:
.
Вынесем в знаменателе х за скобки 
и сократим дробь на х: 
.
Видим, что при подстановке х =0 числитель и знаменатель не обращаются в 0, следовательно, теперь предел вычисляется простой подстановкой:
= 
= 
=-8.
Ответ: =-8.
