Задача 2.4.1. Три фермерских хозяйства А1, А2, А3 ежедневно могут доставлять в магазины соответственно 70, 50 и 60 ц картофеля для обеспечения четырёх торговых точек: В1, В2, В3, В4. Стоимость перевозки 1 ц картофеля и потребность торговых точек в картофеле указаны в табл. 2.4.1.
Таблица 2.4.1. Исходные данные транспортной задачи
| Фермерские хозяйства | Затраты на перевозку 1 ц картофеля по торговым точкам | Запасы картофеля, ц | |||
| В1 | В2, | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потребности в картофеле, ц |
Определить план поставки картофеля в каждую точку для удовлетворения потребностей, чтобы суммарные транспортные издержки были минимальными.
Решение.
1. Проверяем наличие закрытости транспортной модели.
Задача называется закрытой, если a 1 + a 2 +…+ am = b 1+ b 2 +…+ bn.
Если a 1 + a 2 +…+ am 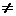 b 1+ b 2 +…+ bn, то задача называется открытой. a 1, a 2, …, am – запасы картофеля у
b 1+ b 2 +…+ bn, то задача называется открытой. a 1, a 2, …, am – запасы картофеля у  поставщиков, b 1, b 2,…, bn – потребности потребителей.
поставщиков, b 1, b 2,…, bn – потребности потребителей.
В нашем случае  ,
,
 .
.
Следовательно задача открытая.
Составим математическую модель задачи.
Введём переменные  –количество картофеля, которое планируется перевозить от i -го фермерского хозяйства к j -й торговой точке (например, х 11 –количество картофеля, которое планируется перевозить от первого фермерского хозяйства к первой торговой точке), Z – суммарные транспортные издержки, которые надо минимизировать:
–количество картофеля, которое планируется перевозить от i -го фермерского хозяйства к j -й торговой точке (например, х 11 –количество картофеля, которое планируется перевозить от первого фермерского хозяйства к первой торговой точке), Z – суммарные транспортные издержки, которые надо минимизировать:

С первого фермерского хозяйства вывозится  ц картофеля и так как задача открытого типа, запасы картофеля больше потребностей, то эта величина не превосходит 70 ц, что записывается в виде неравенства
ц картофеля и так как задача открытого типа, запасы картофеля больше потребностей, то эта величина не превосходит 70 ц, что записывается в виде неравенства  . Количество привезённого картофеля на первую торговую точку равно
. Количество привезённого картофеля на первую торговую точку равно  и оно равно 20 ц, т.е х 11+ х 21+ х 31 = 1700. Поступая аналогично по остальным фермерским хозяйствам и торговым точкам, получаем математическую модель задачи:
и оно равно 20 ц, т.е х 11+ х 21+ х 31 = 1700. Поступая аналогично по остальным фермерским хозяйствам и торговым точкам, получаем математическую модель задачи:


Так как спрос больше потребления, то вводим фиктивного потребителя с потребностью равнёй 180 – 160 =2 0 ц и тарифами перевозок равными нулю. Для этого в матрицу транспортной задачи вводим дополнительный столбец, соответствующую фиктивному потребителю с потребностями  и тарифами перевозок
и тарифами перевозок 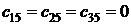 .
.
Для удобства данные запишем в виде табл. 2.4.2.
Таблица 2.4.2. Закрытая транспортная задача примера 2.4.2
| bj ai | |||||
2. Методом северо-западного угла находим начальный опорный план. Сущность метода северо-западного угла состоит в том, что максимально возможные поставки последовательно вводятся в северо-западную клетку таблицы.
У первого поставщика берём 20 ц картофеля и отдаём их первому потребителю. 20 записываем в клетку (1;1). Оставшиеся 50 ц картофеля даём второму потребителю. Второму потребителю надо ещё 30 ц картофеля. Его берём у второго поставщика. Оставшиеся 20 ц картофеля у второго поставщика распределяем третьему потребителю. От третьего поставщика 40 ц отдаём третьему потребителю и 20 ц четвёртому.
Таблица 2.4.3. Первоначальное распределение
| bj ai | ||||||||||||
Проверяем баланс по каждой строке и каждому столбцу.
3. Проверяем распределение на вырожденность. Заполненных клеток должно быть m + n –1=3+5–1=7. Мы получили шесть заполненных клеток. Такое распределение называется вырожденным. Для того, чтобы сделать распределение невырожденным, ставят поставку объемом равным нулю в клетку, которая образует с другими заполненными так называемую цепочку (цикл) перераспределения. Это означает, что от каждой заполненной клетки можно перейти в любую другую заполненную клетку перемещаясь только горизонтально и вертикально. делая повороты только в заполненных клетках. В одну незаполненную клетку (3;4) ставим 0 и считаем ее заполненной. Ноль можно ставить не в любую незаполненную клетку. В нашем случае ноль нельзя ставить в клетки (1;3) и (2;1).
Получили начальное распределение
 ,
,
Z (X 1) = 20·6+50·5+30·4+20·6+40·8= 930 (грн.).
4. Проверяем полученный план на оптимальность. Проверка текущего опорного плана на оптимальность осуществляется методом потенциалов. Находим потенциалы. Каждому поставщику и потребителю ставим в соответствие числа  , называемые потенциалами таким образом, чтобы их сумма равнялась тарифам соответствующих заполненных клеток.
, называемые потенциалами таким образом, чтобы их сумма равнялась тарифам соответствующих заполненных клеток.
 если (i;j)
если (i;j)  заполненная клетка.
заполненная клетка.
Таблица 2.4.4. Потенциалы и оценки оптимальности
| bj ai | ui | ||||||||||||
| u 1 = 0 | |||||||||||||
| [0] | [  3] 3] | [  2] 2] | |||||||||||
u 2 =  1 1 | |||||||||||||
[  4] 4] |   20 20 |  0 0 | [  3] 3] | ||||||||||
| u 3 = 2 | |||||||||||||
| [3] | [  2] 2] |  [6] [6] | |||||||||||
| vj | v 1 = 6 | v 2 = 5 | v 3 = 7 | v 3 = 6 | v 4 =  2 2 | ||||||||
Для нахождения потенциалов получаем систему уравнений

Система состоит из семи уравнений с восьмью неизвестными. Она неопределённая, то есть имеет бесконечное множество решений. Один из потенциалов приравниваем к нулю, а остальные находятся однозначно из этой системы. Пусть  . Тогда из первого уравнения находим
. Тогда из первого уравнения находим 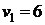 , из второго
, из второго 
 и т.д. Систему можно не выписывать, а значения потенциалов находить непосредственно в таблице.
и т.д. Систему можно не выписывать, а значения потенциалов находить непосредственно в таблице.
5. Находим оценки незаполненных клеток по формуле
 :
:

Их значения записываем в клетках таблицы в нижнем левом углу. Величины груза выделены жирным шрифтом, а значения оценок выделены квадратными скобками. Оценка 3 в клетке (3;1) показывает, что если в эту клетку поместить единицу груза, то стоимость перевозок уменьшится на три гривны. Действительно,для сохранения баланса с клетки (3;4) необходимо отнять единицу груза, в клетку (2;4) необходимо прибавить единицу груза, с клетки (2;2) необходимо отнять единицу груза, в клетку (1;2) необходимо добавить единицу груза, с клетки (1;1) отнять единицу груза. Стоимость перевозки будет соответственно меняться:  , т.е. уменьшиться на 3 грн.
, т.е. уменьшиться на 3 грн.
Отсюда следует, что текущий опорный план будет оптимальным, если для всех незаполненных клеток оценки будут неположительными:
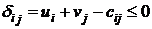
6. Начальный план не является оптимальным, поскольку имеются положительные оценки для пустых клеток. Переходим к новому опорному плану. Переход осуществляется заполнением клетки, которой соответствует наибольшая положительная оценка оптимальности. В нашем случае это клетка (3;3). Для клетки (3;3) строим цикл пересчёта (цепочку перераспределения). Циклом для незаполненной клетки называется последовательность заполненных клеток, в которые поочерёдно добавляется и вычитается груз для сохранения баланса, если в незаполненную клетку поместить некоторый груз. Для каждой свободной ячейки всегда существует только одна цепочка перераспределения. Она составляется таким образом, что на каждом углу цепочки стоят заполненные клетки, а один угол цепочки находится в клетке, куда осуществляется перераспределение.
 |
Рис. 2.4.1. Цикл перераспределения для клетки (3;3)
7. Определяем груз ρ, который будем перемещать по циклу, он равный минимуму грузов стоящих в клетках, в которых он вычитается от объемов в клетках
ρ = min (40,20) = 20.
8.Составляем новую таблицу. Клетка (3;3) заполняется, а клетка (2;3) освобождается. Так как в клетку (3;3) будем ставить груз равный 20 ц, то значение целевой функции при втором распределении уменьшится следующим образом:
 .
.
Таблица 2.4.5. Потенциалы и оценки оптимальности второго плана
| bj ai | ui | ||||||||||||
| u 1 = 0 | |||||||||||||
  20 20 |  50 50 | [  6] 6] | [  3] 3] | [  2] 2] | |||||||||
 |  | u 2 = -1 | |||||||||||
[  4] 4] | [  6] 6] | [  3] 3] | |||||||||||
| u 3 = 2 | |||||||||||||
 [3] [3] | [  2] 2] | ||||||||||||
| vj | v 1 = 6 | v 2 = 5 | v 3 = 1 | v 3 = 6 | v 4 =  2 2 | ||||||||

Z (X 2) = 20·6+50·5+30·4+20·5+20·3+20·8= 810 (грн.)
 2017-11-30
2017-11-30 2344
2344
