Двойственный симплекс-метод состоит в том, что переход от одного базисного решения к следующему осуществляется с помощью анализа двойственных задач. При этом свободные члены могут быть временно и отрицательными. Этот метод позволяет избавиться от необходимости введения искусственных переменных.
Решать ЗЛП двойственным методом начинают, как всегда, сведением ее к канонической форме и образованию полного единичного базиса методом Жордана-Гаусса. Знаки свободных членов могут быть произвольными. Если задача на max, то ее можно и оставлять на max.
Решение задач с помощью двойственного симплекса разделяется на два этапа. Рассматривается случай 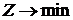 .
.
І-й этап.Достигается условие оптимальности.
1. Разрешающая строка выбирается произвольно. Пусть это будет r -я строка.
2. Разрешающий столбец выбирается по min небазисного двойственного отношения:
 ,
,
 – разрешающий элемент.
– разрешающий элемент.
Итерации продолжаем до тех пор, пока получим условия оптимальности, то есть получим псевдоплан.
Псевдопланом называется базисное решение, для которого выполняются условия оптимума.
Если в псевдоплане все компоненты неотрицательные, то решение задачи закончено.
ІІ-й этап. Псевдоплан преобразовывают в план
1. Разрешающую строку выбираем по наименьшему отрицательному свободному члену. Пусть это будет p -ая строка.
2. Разрешающий столбец выбираем по min двойственного симплексного отношения:
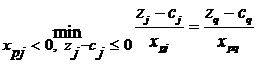 ,
,
 . – разрешающий элемент.
. – разрешающий элемент.
Процесс продолжается до тех пор, пока получим оптимальное решение.
Замечание. Если на некотором этапе в некотором уравнении получится свободный член отрицателен, а среди коэффициентов при неизвестных в этом уравнении отрицательных нет, то задача не имеет решения.
Это очевидно, так как левая и правая части уравнения будут иметь разные знаки.
В литературе под двойственным симплекс-методом часто понимают только второй этап, то есть в задаче псевдоплан уже найден.
Задача 2.3.2. Решить двойственным симплексом ЗЛП

Решение. Переходим к каноническому виду.

Задачу решаем двойственным симплекс-методом.
Таблица 2.3.8
| ↓ | ||||||||
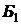
| 
| 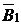
| 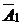
| 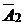
| 
| 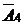
| 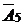
| |
 1 1
|  1 1
|  2 2
| ||||||

|  2 2
| |||||||
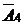
|  4 4
|  1 1
| ||||||
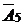
|  6 6
|  1 1
| [  2] 2]
| |||||

|  16 16
|  1 1
|  1 1
|
В данном примере условия оптимальности для начального базисного решения выполняются. Поэтому первого этапа выполнять не надо. Имеем псевдоплан  .
.
Делаем пересчёт симплекс-таблицы. Разрешающую строку выбираем по наименьшему свободному члену, наименьший свободный член  (
( 6). Разрешающий столбец выбираем по минимуму двойственного симплексного отношения:
6). Разрешающий столбец выбираем по минимуму двойственного симплексного отношения:
 .
.
Следовательно, в базис вводим вектор 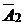 , а из базиса выводим вектор
, а из базиса выводим вектор 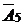 .
.
Выполняем такие итерации пока все свободные члены станут неотрицательными.
Таблица 2.3.9
| ↓ | |||||||||
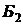
| 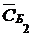
| 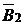
| 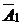
| 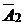
| 
| 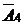
| 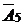
| ||
 1 1
|  1 1
|  2 2
|
Наименьший
свободный член  7 7
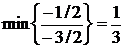
| ||||||

|  2 2
| 1/2 |  1 1
| 1/2 | |||||
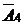
|  7 7
| [  3/2] 3/2]
| 1/2 | ||||||
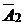
|  1 1
| 1/2 |  1/2 1/2
| ||||||

|  13 13
|  1/2 1/2
|  1/2 1/2
|
Таблица 2.3.10
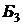
| 
| 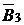
| 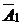
| 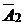
| 
| 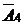
| 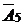
| Все условия
оптимальности
выполнены.
Ответ: 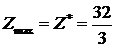
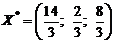
|
 1 1
|  1 1
|  2 2
| ||||||

|  2 2
| 8/3 | 1/3 | 2/3 | ||||
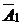
|  1 1
| 14/3 |  2/3 2/3
|  1/3 1/3
| ||||
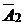
|  1 1
| 2/3 | 1/3 |  1/3 1/3
| ||||

|  32/3 32/3
|  1/3 1/3
|  2/3 2/3
|
|
Двойственная задача

 2017-11-30
2017-11-30 713
713

 ,
,  .
Контроль:
.
Контроль: 







