2017-11-30
1322
Задача 2.3.1. Решить задачу методом искусственного базиса и с помощью «Поиска решений», написать двойственную задачу и записать её решение.
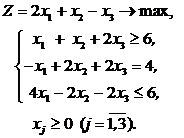
Решение. Переходим к канонической форме модели. Для этого с левой части первого уравнения вычитаем балансовую переменную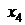 
, а в левую часть третьего уравнения прибавляем балансовую переменную 
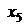. В целевую функцию их не дописываем (дописываем с нулевыми коэффициентами). Получаем задачу линейного программирования в канонической форме
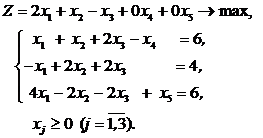
При решении задачи линейного программирования симплекс-методом предполагалось, что в каждом уравнении есть базисная переменная. Это переменная, которая является изолированной, т.е., переменная, которая входит лишь в одно уравнение с коэффициентом 1 и отсутствует в остальных уравнениях.
Если этого нет, то базисные переменные можно формально дописать в соответствующие уравнения.
В первое и второе уравнения прибавляем искусственные переменные х 6 и х 7 с коэффициентом равным единице. В целевую функцию их дописываем с большим отрицательным коэффициентом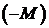 
. Получим расширенную задачу с полным единичным базисом.
|
|
|
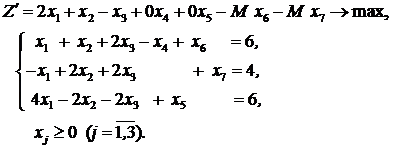
Задачу решаем симплекс методом. Ясно, что искусственные переменные должны равняться нулю для того, чтобы выполнялись условия равенства системы ограничений. Если среди них окажутся ненулевые, то исходная задача несовместна. Иначе целевая функция расширенной задачи будет неограниченно уменьшаться с ростом М и не сможет достичь максимума.
Расширенная задача решается обычным симплекс-методом. Числа в индексной строке имеют вид a+bM. Для их записи в симплексной таблице индексную строку разбиваем на две подстроки и записывают их в виде 
. Другими словами индексную строку записывают в двух уровнях: в (m +1) строку вносят а, а в (m +2) b. Знак числа определяется знаком числа b если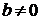 
. Поэтому сначала направляющий столбец выбирают по нижней строке, а после перевода всех искусственных переменных в свободные оптимизация производится по верхней индексной строке.
Если все искусственные векторы вышли из базиса, то получаем систему уравнений равносильную системе уравнений исходной задаче.
При использовании метода искусственного базиса в качестве критерия надо руководствоваться следующим правилом:
Если оптимальное решение М -задачи содержит искусственные переменные или М -задача неразрешима, то исходная задача так же неразрешима.
Замечание. Если m +2 индексная строка в результате преобразований превращается в нулевую (с неположительными оценками искусственных векторов), то это свидетельствует о том, что построен начальный опорный план исходной задачи и дальнейшая оптимизация производится по предпоследней индексной строке.
|
|
|
Имеем начальный опорный план
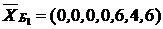и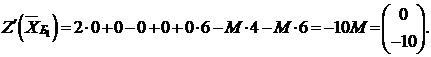 
Проверяем полученный план на оптимальность. Для этого составляем симплекс-таблицу (табл. 2.3.1).
Таблица 2. 3.1
| ¯ | |||||||||||||
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||
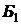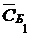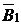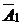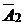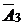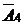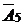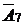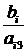| –1 | – М | – М | |||||||||||
|
| – M | –1 |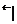 
| ||||||||||
|
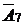| – M | –1 | [2] | (–1) (1) | |||||||||
|
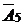| –1 | –2 | – |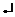 
| |||||||||
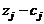| –2 | –1 | |||||||||||
| –10 | –3 | –4 |
Покажем как находится индексная строка.
, 
,
,
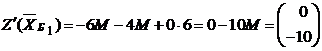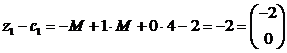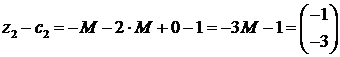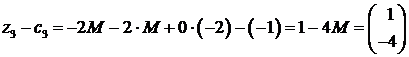
и так далее.
План будет оптимальным, если все оценки в индексной строке положительны или нулевые, т. е.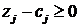 
.
Если находится минимум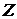 
, то в целевую функцию искусственные переменные дописываются с большим положительным числом 
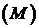. Целевая функция достигнет минимального значения, если все оценки будут неположительными 
.
Первый план не оптимален. В нижней индексной строке наименьшую отрицательную оценку имеет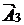 
. Вектор, выводимый из базиса определяем по симплексному отношению 
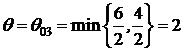. Из базиса выводим вектор 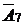. Составляем новую симплекс-таблицу.
После выведения из базиса столбцов, которые отвечают искусственным переменным, эти столбцы дальше можно не вычислять (они обведены двойной линией), но при рассмотрении двойственных задач их обязательно вычисляют.
Составляем вторую симплекс-таблицу
Таблица 2.3.2
| ¯ | |||||||||||||
| 
| 
|
|
|
|
|
|
|
| 
| |||
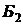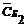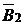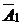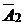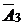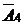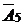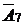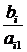| –1 | – М | – М | |||||||||||
|
| – M | [2] | –1 | –1 | –1 | (1/4)(-3/2) | |||||||
|
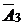| –1 |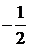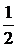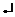 
| 
| – | |
| ||||||||
|
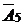| 10/3 |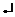
| |||||||||||
|
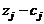| –2 |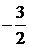 
| –2 |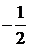
| |||||||||
| –2 | –2 |
Второй план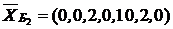 
тоже не оптимальный, вектор 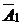имеет отрицательную оценку. Составляем третью симплекс-таблицу. В базис вводим вектор 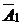, из базиса выводим вектор по симплексному отношению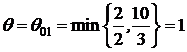 
.
Таблица 2.3.3
| 
| 
|
|
|
|
|
|
|
| 
| |
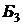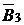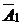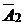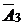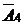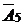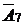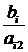| –1 | – М | – М | |||||||||
|
|
|
|
|
| – |
| |||||
|
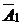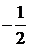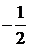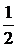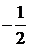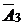| –1 |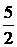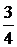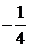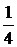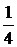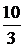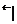 
| 
| 
| 
|
| 
| |
|
| |||
|
| 
| 
|
|
| 
|  
| |||||
|
|
| 
| 
|
| 
| ||||||
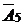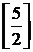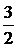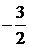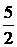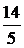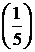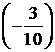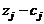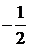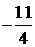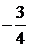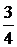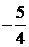Третий план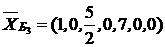 
тоже не оптимальный, вектора 
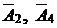имеют отрицательные оценки. Составляем четвёртую симплекс-таблицу. В базис вводим вектор 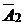, из базиса выводим вектор 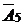по симплексному отношению 
.
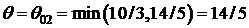Таблица 2.3.4
| 
| 
|
|
|
|
|
|
|
| |
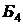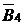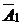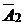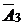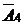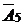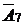| –1 | – М | – М | ||||||||
|
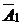| 12/5 | –1/5 | 1/5 | 1/5 | ||||||
|
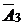| –1 | 2/5 | –7/10 | –3/10 | 7/10 | –1/2 | ||||
|
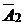| 14/5 | 3/5 | 2/5 | –3/5 | ||||||
|
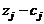| 36/5 | 9/10 | 11/10 | –9/10 | 3/2 | |||||
| 
| 
| 
|
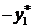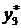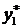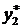Четвёртый план оптимальный.
, 
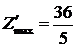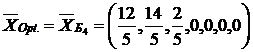. Все искусственные переменные равны нулю, поэтому значения начальных переменных определяют оптимальный план.
Ответ.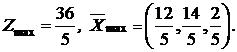 
Решим задачу с помощью Поиска решений в Excel
Решение состоит из двух этапов:
ввести, согласно стандартного приёма, формулы математической модели задачи в Excel;
в диалоговом режиме провести решение задачи по выбранной программе «Поиск решения».
1. Набрать исходные данные ЗЛП в произвольном месте таблицы Excel, как показано в табл. 2.3.5. Клетки D2:D4, где должны находиться знаки ограничений, оставляем свободными (они обведены двумя линиями). В клетке D 1 (обведённой жирной линией) будет находиться значение целевой функции. В клетках: A5: C5 (обведённых жирной штриховой линией) будут находиться значения переменных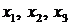 
, на них в процессе решения будет делаться абсолютная ссылка.
|
|
|
Таблица 2.3.5. Данные примера 2.3.1, внесённые в Excel
| A | B | C | D | E | |
| 1 | –1 | ||||
| 2 | |||||
| 3 | –1 | ||||
| 4 | –1 | –2 | |||
| 5 |
По общим правилам вводим формулы математической модели задачи.
Вводим зависимости для целевой функции и ограничений. Для этого курсор ставится в клетку D1 и выполняются действия: «Вставка»; «Функция»; «Математические»; «СУММПРОИЗ»; «ОК».
В строку «Массив 1» вводится A1:C1; в строку «Массив 2» вводится A5:C5; чтобы на массив A5:C5 была абсолютная ссылка, надо нажать F4, когда этот массив выделен; возле номеров второго массива появится знак $;«OK».
Протянуть “маленький” + вниз по клеткам, выделенных двойными линиями. В этих клетках появятся нули. Таблица будет иметь вид
Таблица 2.3.6
| A | B | C | D | E | |
| 1 | –1 | ||||
| 2 | |||||
| 3 | –1 | ||||
| 4 | –1 | –2 | |||
| 5 |
2. Запустись команду «Поиск Решения »: «Сервис»; «Поиск решения» (если «Поиск Решения» нет, то в надстройке поставить галочку возле Поиск Решения); OK.
Дальше работаем в диалоговом режиме. Действия, которые надо выполнять перечислим кратко: установить целевую ячейку D1; Указать максимальное значение; «Изменяя ячейки» A5:C5; «Добавить»; в ссылке на ячейку вводится ячейка D2, выделенная двумя линиями, знак неравенства оставляем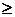 
, в ограничения выделяем клетку F2 с числом 6; «Добавить»; в ссылке на ячейку вводится ячейка D3, выбираем знак «=», ограничения выделяем клетку F3 с числом 4; «Добавить»; в ссылке на ячейку вводится ячейка D4, знак неравенства оставляем 
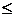, в ограничения выделяем клетку F4 с числом 6;. «ОК».
После этих действий экран будет иметь вид:
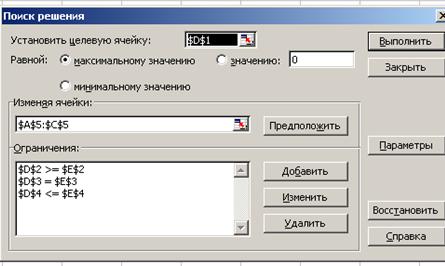
Рис. 2.3.1
«Параметры»;«Линейная модель»;«Неотрицательные значения»;«ОК»;«Выполнить»;«Сохранить найденное решение»;«Выделить Результаты»;«Устойчивость»;«Пределы»;«ОК».
|
|
|
В результате получим решение и его анализ:
Таблица 2.3.7. Решение задача 2.3.1
| A | B | C | D | E | |
 1
| 7,2 | ||||
| 1
| |||||
| 1
| 2
| ||||
| 2,4 | 2,8 | 0,4 |
