Задача 2.5.1. Задача о распределении капитальных вложений
1. Постановка задачи. Концерн, состоящий из 4 крупных предприятий машиностроения решил выделить на их реконструкцию 500 тыс. $. Эффективность функционирования  го предприятия после его реконструкции представлена функциями
го предприятия после его реконструкции представлена функциями 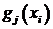 , где
, где  размер выделенной ему суммы и определена в табл. 2.5.1.
размер выделенной ему суммы и определена в табл. 2.5.1.
Таблица 2.5.1
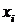
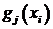
| ||||||
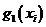
| ||||||

| ||||||
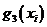
| ||||||
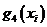
|
Необходимо распределить капиталовложения между предприятиями таким образом, чтобы эффективность работы всех предприятий была максимальной.
2. Построим математическую модель задачи.
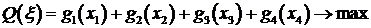
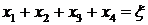
 .
.
3. Рекуррентное соотношение Беллмана для нахождения условно-опти- мальных управлений:
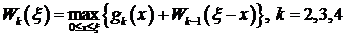 0,
0,
где  максимальная эффективность
максимальная эффективность 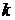 предприятий, если им выделено
предприятий, если им выделено  капиталовложений.
капиталовложений.
4. Решение задачи.
Если мы выделили все средства 1-му предприятию, то по таблице 1 видим, что общий доход будет составлять 43 ед.
Выделим средства первому и второму предприятию. Тогда, пользуясь рекуррентным соотношение Беллмана получим условно-оптимальные управления следующие:
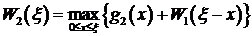
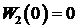 .
.
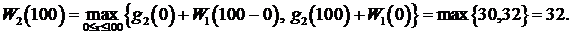
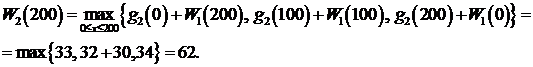
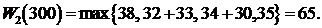
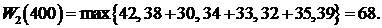
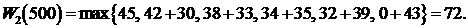
Тогда 
Для удобства расчетов составлены таблицы:
Таблица 2.5.2


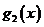
| |||||||
 0 0
| |||||||
| 32* | 62* | 65* | ´ | ||||
| 67* | ´ | ´ | |||||
| ´ | ´ | ´ | |||||
| 72* | ´ | ´ | ´ | ´ | |||
| ´ | ´ | ´ | ´ | ´ |
Выпишем в таблицу условно-оптимальное управление на втором шаге.
Таблица 2. 5.2а

| ||||||
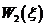
| ||||||
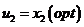
|
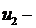 оптимальное выделение средств второму предприятию при распределении их между двумя первыми.
оптимальное выделение средств второму предприятию при распределении их между двумя первыми.
Для трех предприятий:
Таблица 2.5.3
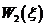
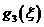
| |||||||
 0 0
| 32* | 62* | |||||
| 81* | ´ | ||||||
| 89* | ´ | ´ | |||||
| 95* | ´ | ´ | ´ | ||||
| ´ | ´ | ´ | ´ | ||||
| ´ | ´ | ´ | ´ | ´ |
Таблица 2.5.3 а

| ||||||
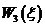
| ||||||
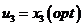
|
 оптимальное выделение средств третьему предприятию при распределении их между тремя первыми.
оптимальное выделение средств третьему предприятию при распределении их между тремя первыми.
Для четырех предприятий:
Таблица 2.5.4
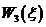
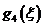
| |||||||
 0 0
| 32* | 62* | |||||
| 90* | 109* | 117* | ´ | ||||
| ´ | ´ | ||||||
| ´ | ´ | ´ | |||||
| ´ | ´ | ´ | ´ | ||||
| ´ | ´ | ´ | ´ | ´ |
Таблица 2.5.4а

| ||||||
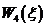
| ||||||
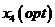
|
Таким образом, из табл. 2.5.4. а видим, что max эффект составляет 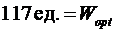 . Теперь будем находить безусловно-оптимальное управление. Для этого будем использовать таблицы 2.5.2а, 2.5.3а 2.5.4а. Максимальный эффект получается, если четвертому предприятию мы выделим 100 тыс. т.е
. Теперь будем находить безусловно-оптимальное управление. Для этого будем использовать таблицы 2.5.2а, 2.5.3а 2.5.4а. Максимальный эффект получается, если четвертому предприятию мы выделим 100 тыс. т.е 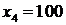 .
.
Если трем предприятиям выделим 400 тыс. $, то оптимальный эффект будет при выделении третьему предприятию 300 тыс. $, т.е.  (из табл. 2.5.3а).
(из табл. 2.5.3а).
Теперь видно, что для первого и второго предприятия остается 100 тыс. $. Из таблицы 2.5.2а видим, что max эффект при выделении первым двум предприятиям 100 тыс. будет, если второму предприятию мы выделим 100 тыс. $, т.е. 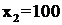 . Тогда
. Тогда 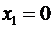 .
.
Ответ:  ;
; 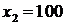 ;
;  ;
; 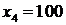 и
и 
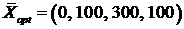 .
. 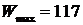 .
.
 2017-11-30
2017-11-30 608
608







