Во многих динамических задачах время рассматривается непрерывно, или как дискретная величина. Задачи такого типа называются многошаговыми (многоэтапными) задачами оптимизации. Их можно решать методом динамического программирования.
В многошаговых задачах оптимизации время принимает дискретные значения: 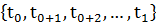 .
.
Состояние системы в момент времени 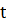 задается вектором:
задается вектором: 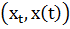 , где
, где 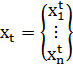 ,
, 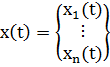 .
.
В уравнении в момент времени 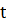 задается
задается 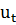 дискретными значениями.
дискретными значениями.
Рассмотрим простейшую многошаговую систему - одношаговую систему. Начальное состояние системы записывается известным в ектором состояния 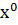 . Выбор некоторого управления
. Выбор некоторого управления 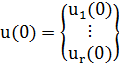 определяет переход системы из
определяет переход системы из 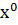 в состояние
в состояние 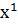 . Этот переход описывается соотношениями:
. Этот переход описывается соотношениями: 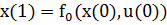 .
.
Для многошаговых систем будем иметь
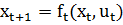 , где
, где 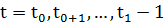 ; (11)
; (11)
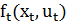 – вектор, составленный из непрерывно дифференцируемых функций текущего состояния
– вектор, составленный из непрерывно дифференцируемых функций текущего состояния 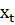 и текущих значений управления
и текущих значений управления 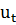 .
.
Блок-схема многошагового процесса имеет вид (Рис.2): 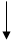
|

|
|

|
|


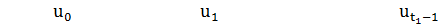




 …
… 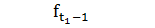
Рис.2
Здесь 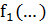 вектор, составленный из непрерывно дифференцируемых функций текущего состояния и текущих значений управляющих параметров.
вектор, составленный из непрерывно дифференцируемых функций текущего состояния и текущих значений управляющих параметров.
Предполагаем, что заданное начальное состояние 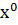 - фиксированное. Требуется найти такую последовательность векторов
- фиксированное. Требуется найти такую последовательность векторов 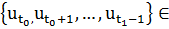 фиксированной области управления
фиксированной области управления 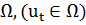 , где
, где 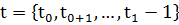 , которая максимизирует целевую функцию
, которая максимизирует целевую функцию
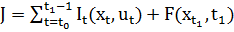
Таким образом, данная задача аналогична задачи оптимального управления с непрерывным временем – дискретная задача – многошаговая задача оптимального управления.
Подход динамического программирования в данном случае состоит в том, что решаемая задача “погружается ” в более широкий класс задач, описываемых рядом параметров, и вслед за этим, используя принцип оптимальности Беллмана, определяется основное рекуррентное соотношение.
Первый подход.
Возьмем в качестве параметров многошаговой задачи оптимизации начальный момент времени 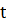 и начальное состояние
и начальное состояние 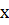 . Тогда функция оптимального поведения равна оптимальному значению целевой функции J задачи с начальным состоянием
. Тогда функция оптимального поведения равна оптимальному значению целевой функции J задачи с начальным состоянием 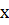 и начальным моментом времени
и начальным моментом времени 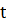 . Тогда оптимальное значение целевой функции исходной задачи равно:
. Тогда оптимальное значение целевой функции исходной задачи равно: 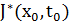 . Согласно принципу оптимальности Беллмана:
. Согласно принципу оптимальности Беллмана:
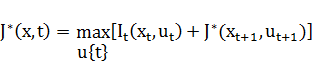 , где
, где 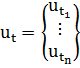 ,
, 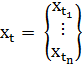 .
.
Это означает, что оптимальное значение целевой функции с наименьшим состоянием 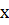 и наименьшим моментом времени
и наименьшим моментом времени 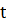 равно оптимальному значению функции
равно оптимальному значению функции 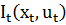 в момент времени
в момент времени 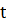 и оптимальному значению функции оптимального поведения
и оптимальному значению функции оптимального поведения 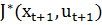 в момент времени
в момент времени 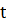 . Можно представить все рекуррентные соотношения в виде:
. Можно представить все рекуррентные соотношения в виде:
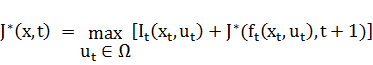 .
.
Для этого соотношения граничное условие будет: 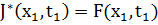 - – показывает, что оптимальное значение целевой функции с начальным состоянием
- – показывает, что оптимальное значение целевой функции с начальным состоянием 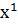 в момент времени
в момент времени 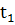 равно (совпадает) со значением функции конечных параметров, рассчитанных при
равно (совпадает) со значением функции конечных параметров, рассчитанных при 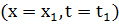 . Данная задача аналогична задачи оптимального управления с непрерывным временем.
. Данная задача аналогична задачи оптимального управления с непрерывным временем.
Второй подход.
Другой подход при решении многошаговых задач оптимизации состоит в том, что в качестве характеристических параметров выбираются не начальные состояния и не начальный момент времени, а начальное состояние и промежуток времени, остающийся до конечного момент времени.
Тогда ФОП 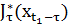 – которая представляет собой оптимальное значение целевой функции с начальным состоянием
– которая представляет собой оптимальное значение целевой функции с начальным состоянием 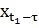 , разворачивающаяся в промежутке протяженностью
, разворачивающаяся в промежутке протяженностью 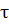 . Оптимальное значение целевой функции исходной задачи соответственно равно:
. Оптимальное значение целевой функции исходной задачи соответственно равно: 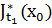 – когда
– когда 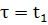 . В этом случае последовательность решений определяется методом динамического программирования в порядке, обратном тому, который рассматривается до сих пор.
. В этом случае последовательность решений определяется методом динамического программирования в порядке, обратном тому, который рассматривается до сих пор.
Первым членом этой последовательности является: 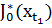 , то есть оптимальное значение целевой функции с временным промежутком нулевой протяженности, начинающейся (и заканчивающейся) в
, то есть оптимальное значение целевой функции с временным промежутком нулевой протяженности, начинающейся (и заканчивающейся) в 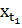 . Оптимальное значение целевой функции этой задачи равно функции конечных параметров:
. Оптимальное значение целевой функции этой задачи равно функции конечных параметров: 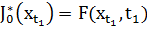 .
.
Рассмотрим 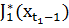 – оптимальное значении целевой функции, задачи с промежутком равным одной единице времени
– оптимальное значении целевой функции, задачи с промежутком равным одной единице времени 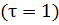 , начинающегося в
, начинающегося в 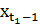 . Эта задача называется первым шагом.
. Эта задача называется первым шагом.
Оптимальное значение в этой задачи определяется как максимум значения суммы той части целевой функции, которая соответствует указанному времени, и оптимальное значение задачи с моментом времени 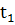 с управляющим вектором
с управляющим вектором 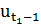 :
:
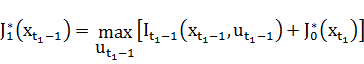 .
.
Используя уравнение перехода: 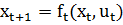 , получаем
, получаем
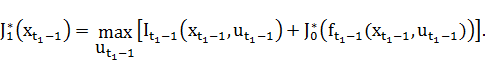
Данный выбор управления на первом шаге согласуется с принципом оптимальности Беллмана, поскольку управление 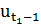 - оптимально, то по отношению к состоянию
- оптимально, то по отношению к состоянию 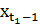 , которое достигается в результате
, которое достигается в результате 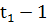 предыдущих выборов управляющих векторов.
предыдущих выборов управляющих векторов.
Аналогично этому, на втором шаге (в задаче с промежутком равным двум промежуткам времени) получим
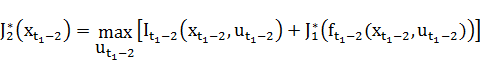 .
.
Общее р екуррентное соотношение на шаге с номером 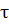 выглядит следующим образом
выглядит следующим образом
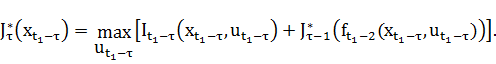
В рассмотренной задаче, оптимальное значение равно: 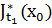 – является оптимальным значением последней задачи в последовательности одношаговых задач оптимизации, описываемых функциональным уравнением, при
– является оптимальным значением последней задачи в последовательности одношаговых задач оптимизации, описываемых функциональным уравнением, при 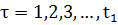 , с граничным условием:
, с граничным условием: 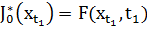 . Вместо того, что бы решать эту задачу методом НЛП (выбирать сразу
. Вместо того, что бы решать эту задачу методом НЛП (выбирать сразу 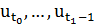 ), то здесь мы решаем последовательность одношаговых задач оптимизации.
), то здесь мы решаем последовательность одношаговых задач оптимизации.
 2017-11-30
2017-11-30 1947
1947

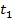 -1)
-1) 






