Теплопроводность через однослойную плоскую стенку

МИНИСТЕРСТВО РОССИЙСКОЙ ФЕДЕРАЦИИ

ПО ДЕЛАМ ГРАЖДАНСКОЙ ОБОРОНЫ,

ЧРЕЗВЫЧАЙНЫМ СИТУАЦИЯМ И ЛИКВИДАЦИИ ПОСЛЕДСТВИЙ

СТИХИЙНЫХ БЕДСТВИЙ

УРАЛЬСКИЙ ИНСТИТУТ ГОСУДАРСТВЕННОЙ ПРОТИВОПОЖАРНОЙ СЛУЖБЫ

 

 

Кафедра физики и теплообмена

 

 

Дисциплина:

ТЕПЛОТЕХНИКА

 

 

Л Е К Ц И Я

 

ТЕМА 13: ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ И ГРАНИЧНЫХ УСЛОВИЯХ ПЕРВОГО РОДА

 

 

Автор:

д.ф.-м.н., профессор П.В. Скрипов

 

 

Екатеринбург 2006

Цели лекции:

 

Учебные: Дать представление о методах решения уравнения теплопроводности при стационарном режиме и граничных условиях первого рода для однородных тел различной формы.

 

Воспитательные: Воспитывать стремление к углубленному изучению предмета; прививать убежденность в практической значимости получаемых в лекционном курсе знаний.

 

Развивающие: Развивать способность творчески воспринимать и конспектировать предоставляемый материал; развивать навыки самостоятельной аналитической работы, умение выделять главное, проводить сопоставление и обобщение.

 

Метод проведения: лекция

Время занятия: 160 минут

Место проведения: аудитория

Материальное обеспечение: раздаточный материал с представлением основных соотношений и графиков

 

ЛИТЕРАТУРА:

1. Теплотехника: Учебник для вузов / А.П. Баскаков, Б.В. Берг, О.К. Витт и др.; под ред. А.П. Баскакова. 2-е изд., перераб. – М.: Энергоатомиздат, 1991. 224 с.

2. Техническая термодинамика: Учебное пособие / В.Н.Королёв, Е.М.Толмачёв. Екатеринбург: УГТУ, 2001. 180 с.

 

ПЛАН ЛЕКЦИИ:

1. Введение в методы решения уравнения теплопроводности при стационарном режиме и граничных условиях первого рода.

2. Однослойная плоская стенка..

3. Многослойная плоская стенка.

4. Эквивалентный коэффициент теплопроводности.

5. Однослойная цилиндрическая стенка.

6. Многослойная цилиндрическая стенка.

7. Шаровая стенка.

 

 

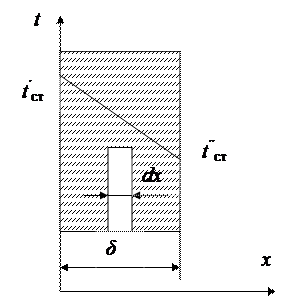
Теплопроводность через однослойную плоскую стенку.

Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля. Для любого конкретного случая к нему надо присоединить не­обходимые краевые условия.

Рассмотрим наиболее распространенный случай — теплопровод­ность через однослойную плоскую стенку, длина и ширина которой бесконечно велики по сравнению с толщиной δ (рис. 2-1). Стенка имеет во всех своих частях оди­наковую толщину, причем температуры поверхно­стей t´ _сти t´´ _ст

поддерживаются постоянными, т. е.

Рис. 2-1.

являются изотермическими поверхностями. Темпе­ратура меняется только в направлении, перпен­дикулярном к плоскости стенки, которое прини­маем за ось х. Коэффициент теплопроводности λ по­стоянен для всей стенки. При стационарном теп­ловом режиме температура в любой точке тела не­изменна и не зависит от времени, т. е. ∂t / ∂τ = 0. Тог­да дифференциальное уравнение теплопроводности, после сокращения коэффициента температуропроводности, принимает вид

.

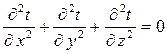Но при принятых условиях первые и вторые производные от t по у и z также равны нулю:

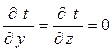и ,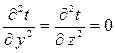

поэтому уравнение теплопроводности можно написать в следующем виде:

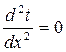. (2-1)

Интегрируя уравнение (2-1), находим

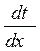= const = А.

После вторичного интегрирования получаем

t = Ах + В.

При постоянном коэффициенте теплопроводности это есть уравнение прямой линии. Следовательно, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.

Найдем постоянные интегрирования А и В. При х = 0температура t = t´ _ст = B; при х = δ температура t = t´´ _ст= Аδ + t´ _ст,откуда

.

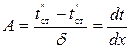Плотность теплового потока найдем из уравнения Фурье (1-7)

,

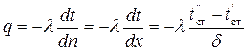или

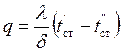Вт/м². (2-2)

Зная удельный тепловой поток, можно вычислить общее количество теплоты, которое передается через поверхность стенки F за время τ:

Q = 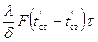Дж(2-3)

Количество теплоты, которое передается теплопроводностью через плоскую стенку, прямо пропорционально коэффициенту теп­лопроводности стенки λ, ее площади F, промежутку времени τ, раз­ности температур на наружных поверхностях стенки (t´ _ст- t´´ _ст) и обратно пропорционально толщине стенки δ. Тепловой поток за­висит не от абсолютного значения температур, а от их разности t ^’_ст — t ^”_ст = Δ t, называемой температурным напором.

Полученное уравнение (2-2) является справедливым для случая, когда коэффициент теплопроводности является постоянной вели­чиной. В действительности коэффициент теплопроводности реальных тел зависит от температуры и закон изменения температуры в стенке выражается кривой линией. Если коэффициент теплопроводности зависит от температуры монотонно, то закон изменения температуры в стенке считают, в первом приближении, линейным.

Уравнение (2-2) можно получить непосредственно из закона Фурье (1-6), считая, что температура изменяется только в направ­лении оси х:

.

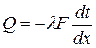Разделив переменные, получаем

.

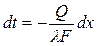Интегрируя последнее уравнение при условии Q = const, на­ходим

.

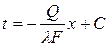Постоянную интегрирования С найдем из граничных условий:

при х = 0температура t = t´ _ст = C;

при x = δ температура t = t´´ _ст = 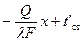, откуда

Q = 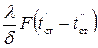Вт.

Введем в уравнение (2-2) поправки на зависимость λ от t, считая эту зависимость линейной:

λ = λ ₀(1 + bt). (а)

В этом случае, подставив в уравнение Фурье вместо λ его зна­чение из формулы (а), получаем

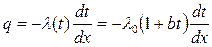. (б)

Разделив переменные и интегрируя в пределах от x = 0 до x = δ в интервале температур от t´ _стдо t´´ _ст,получаем

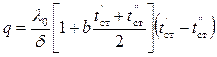. (2-4)

Уравнение (2-4) позволяет определить плотность теплового потока при переменном коэффициенте теплопроводности. В этом уравнении множитель

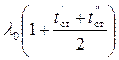является среднеинтегральной величиной коэффициента теплопроводности.

В (2-2) было принято λ = const и равным среднему значению λ _ср. Поэтому, сравнивая уравнения (2-2) и (2-4), получаем

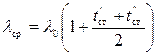. (2-5)

Следовательно, если λ _ср определяется при среднеинтегральной температуре t _{cp.ст. =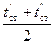} , то формулы (2-2) и (2-4) равнозначны.

При этом плотность теплового потока может определяться из уравнения

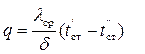Вт/ м².(2-6)