2017-10-25
1394
Основным математическим аппаратом термодинамики является теория дифференциальных пфаффовых форм от двух и более независимых переменных, а также методы преобразования частных производных от одной группы независимых переменных к другой. В общем случае дифференциальная форма записывается в виде
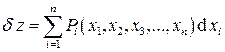. (1.1)
Здесь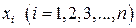 
- набор независимых переменных (в термодинамике - набор независимых параметров состояния системы); d xi - дифференциалы независимых переменных, т.е. бесконечно малые изменения независимых параметров состояния; 
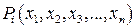- заданные функции независимых переменных. Эти функции представляют собой либо свойства термодинамической системы, либо функции параметров. Выражение (1.1) позволяет получить функцию 
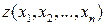интегрированием этой дифференциальной формы вдоль некоторой гиперкривой в пространстве переменных 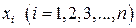. Известно, однако, что в общем случае результат интегрирования (1.1), т.е. конкретный вид функции 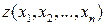, будет зависеть как от выбранного начального состояния (0), так и от пути (γ) перехода системы из этого начального состояния до текущего, т.е. в общем случае решение следует писать в виде 
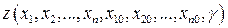. Известно также, что существуют два типа дифференциальных форм, одна из которых, называемая неполным дифференциалом,характеризуется зависимостью решения 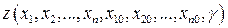от пути интегрирования (γ) и другая, называемая полным дифференциалом, интеграл которого 
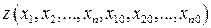не зависит от выбора пути.
|
|
|
Примеров, иллюстрирующих свойства полных и неполных дифференциалов, можно привести множество из различных областей физики, экономики и т.д. В частности, рассмотрим пример с автомобилем, перевозящим груз из какого-либо пункта А, находящегося на географической высоте h A, в пункт Б на высоте h Б. И пусть имеется множество маршрутов, соединяющих эти пункты. Тогда, как известно, работа по поднятию груза с высоты h A на высоту h Б в поле тяжести определится произведением веса груза на разность высот h Б- h A и не будет зависеть от маршрута, т.е. от пути. На каждом малом участке любого из маршрутов малые величины работы по поднятию груза определятся дифференциалом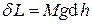 
, который в данном случае будет полным. Что же касается таких величин, как затраты времени, топлива или стоимости перевозки, то они, очевидно, будут зависеть от выбранного маршрута, т.е. от его длины, состояния дорог, режима движения и даже от времени суток. Дифференциалы этих величин, т.е. их малые количества на малых участках разных маршрутов, будут неполными.
Условимся в дальнейшем для полных дифференциалов использовать традиционное обозначение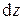 
, а для неполных – 
.
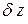Мы будем в дальнейшем рассматривать так называемые простые термодинамические системы, состояние которых однозначно определяется заданием значений двух независимых переменных. В этом случае дифференциальная форма принимает более простой вид
|
|
|
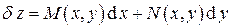. (1.2)
В математике существуют два признака полноты или неполноты дифференциальной формы:
· Интегральный - интеграл по любому замкнутому пути (контуру) от полного дифференциала равен нулю, т.е.
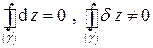; (1.3)
· Дифференциальный - равенство перекрёстных производных в случае полного дифференциала, т.е. если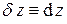 
, то
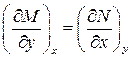. (1.4)
Интегральный признак (1.3) позволяет утверждать, что результатом интегрирования неполного дифференциала от состояния (1) до состояния (2) будет некоторое число z 12, величина которого зависит от выбора пути (γ), т.е.
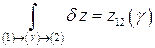. (1.5)
В случае же, если дифференциал является полным, то результат его интегрирования в тех же пределах не будет зависеть от пути (γ), а будет определяться только разностью значений функции z (x, y) в конечном (2) и начальном (1) состояниях:
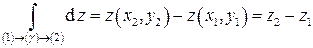. (1.6)
Большое прикладное значение в термодинамике имеет случай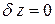 
, т.е. когда
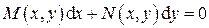. (1.7)
Это выражение есть не что иное, как обыкновенное дифференциальное уравнение первого порядка
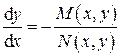, (1.8)
решение которого y = y (x, C) геометрически представляет собой семейство кривых на плоскости переменных (x, y), каждая из которых характеризуется своим значением параметра C. Оказывается, что интегральные кривые в случае двух независимых переменных никогда не пересекаются, кроме, возможно, дискретного набора точек или конечного набора линий. А это говорит о том, что дифференциальная форма 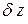, не будучи полным дифференциалом, всегда может быть преобразована в полный умножением на подходящим образом подобранную или вычисленную функцию 
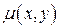, называемую интегрирующим множителем, таким образом, что
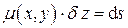. (1.9)
Для непрерывной однозначной функции z (x,y) всегда можно записать полный дифференциал в виде суммы частных дифференциалов
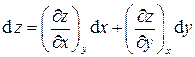, (1.10)
где частные производные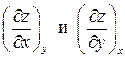 
обычно связаны с физическими свойствами вещества и имеют смысл изменения какого-либо из параметров, например z, при изменении другого параметра, например x, на единицу при условии, что третий параметр, например y, поддерживается постоянным. Во многих случаях экспериментальное нахождение физических свойств веществ, т.е. соответствующих частных производных, либо является весьма трудоёмким, либо вообще невозможно. Мощь термодинамического метода состоит в том, что, опираясь на самые общие законы природы и используя формализм простейших операций с дифференциальными формами, термодинамика позволяет описывать и предсказывать поведение самых разных термодинамических систем при тех или иных воздействиях и при соблюдении тех или иных условий.
В частности, пусть производные 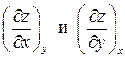сравнительно легко измеряются на опыте, а свойство 
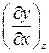для своего измерения требует существенных затрат времени или средств или просто невозможно. Но из (1.10), полагая z = const, d z = 0, имеем
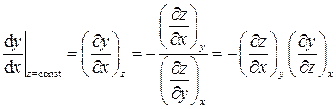. (1.11)
В термодинамике часто оказывается полезным так называемое преобразование Лежандра, основанное на известной формуле дифференциального исчисления
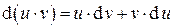. (1.12)
Это преобразование позволяет вводить в рассмотрение новые функции состояния, которые могут оказаться более удобными в практических расчетах и/или иметь более ясный и содержательный физический смысл. Непосредственное использование преобразования Лежандра будет показано на конкретных задачах термодинамики в ходе дальнейшего изложения.
Тема 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕРМОДИНАМИКИ (2)
