Внешние нагрузки в процессе эксплуатации сооружений, как правило, представляют собой не просто случайные величины, но и случайные процессы. Для корректного учета изменяемости нагрузок в исследованиях прочности необходимо статистическое описание их характеристик, позволяющее с достаточной достоверностью решать задачи статики, динамики и устойчивости, и применение методов теории вероятности и теории случайных процессов.
В зависимости от сложности решаемых задач и необходимой точности их решения возможны эмпирические исследования для определения вероятности отказа, когда это связано с превышением некоторого заданного уровня параметра нагрузки S(t) хотя бы один раз в течение интервала времени Т, равного назначенному сроку службы. В этом случае допустимо рассматривать отказ в рамках элементарной теории вероятности. Для этого необходимо знать плотность распределения вероятности p(S/T) максимальных значений параметра нагрузки S(t) в пределах различных интервалов времени наблюдения Т (Т1 < Т2 < Т3) (рис.4.2.).

Рис. 4.2. Изменение плотности распределения вероятности p(S/T) для максимальных значений нагрузки с увеличением времени наблюдения Т
Существенно, что распределения зависят от продолжительности наблюдений. Если разбить время Т на m равных достаточно больших интервалов ∆Т, чтобы корреляция максимумов для двух соседних интервалов была пренебрежимо малой, можно абсолютные максимумы для каждого интервала ∆Т приближенно рассматривать как случайные величины в последовательности независимых испытаний. Тогда плотность вероятности p(S/T) определится по формуле [7]:

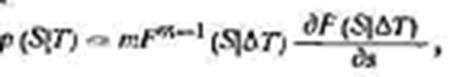
где F(S│∆T) – функция распределения вероятности для максимумов на базе наблюдения, равной ∆ Т.
Рассмотренный выше подход определения статистических характеристик внешнего нагружения предполагает квазистатическое приложение нагрузок и поэтому максимальные значения параметра нагрузки в заданном интервале времени можно считать случайными величинами.
Если параметр нагрузки описывает динамический процесс, то его следует трактовать как случайный процесс с множеством реализаций, каждое из которых характеризуется различным распределением во времени (рис. 4.3.).
Вероятностный анализ распределений и осреднение будет, естественно, зависеть для случайных процессов от интервалов t1 - t2, t1 - t3 и т. д.

Рис. 4.3. Нагрузка как случайный процесс (эргодический)
Для стационарных случайных процессов при Т→ ∞ для каждой реализации характеристики математического ожидания, дисперсии и корреляционных функций при замене интегралов конечными суммами можно получить эмпирически или путем моделирования с необходимой точностью выбирая продолжительность реализации Т [7].
В широком, хотя и не особенно точном понимании, случайным процессом ξ(t) является любой протекающий во времени процесс, управляемый вероятностными законами. Более определенно: случайная функция ξ(t) — это такая функция, значение которой при любом возможном t есть случайная величина.
В математической теории нет никаких оснований к тому, чтобы придавать аргументу t какую-либо определенную интерпретацию.
Принято называть ξ(t) случайным (или стохастическим, или вероятностным) процессом, если t меняется непрерывно, и случайной последовательностью (процессом с дискретным параметром, с дискретным временем), если t принимает счетное множество значений. Термин «случайная функция» охватывает оба эти случая, т. е. применяется тогда, когда характер изменения t произволен.
В свою очередь множество возможных значений х самой случайной функции ξ(t) тоже может быть как непрерывным, так и дискретным. Таким образом, имеются четыре разновидности случайной функции в соответствии с четырьмя комбинациями дискретности и непрерывности х и t. Иногда все эти разновидности называют случайными процессами, говоря о дискретном или непрерывном процессе (в зависимости от характера х) с дискретным или непрерывным временем t. Разумеется, возможны и смешанные — дискретно-непрерывные — процессы, но изучать удобней каждый из этих видов в отдельности
Если аргумент t принимает конечное множество значений t1, t2, t3,…….. tn, то случайная последовательность сводится, очевидно, к совокупности n случайных величин ξ(t1), ξ(t2), ξ(t3),……… ξ(tn), т. е. может быть интерпретирована как n-мерная случайная величина, задаваемая, как обычно, своим n-мерным распределением вероятности ω(x1, x2, ……xn). Если же множество значений t бесконечно (счетно или непрерывно), то мы выходим за рамки классической теории вероятностей и необходимо специально определить, как в этом случае надо понимать задание случайной функции ξ(t).
Беря за исходный пункт множество всех возможных реализаций случайной функции, можно получить исчерпывающую ее характеристику заданием распределения вероятностей этих реализаций. Равносильный, но по форме отличный подход, принадлежащий Е. Е. Слуцкому, опирается на то, что ξ(t) при каждом фиксированном значении t есть случайная величина. Эта
величина полностью задана, если известно ее распределение

т. е. известна мгновенная плотность вероятности ω1 (t,x) вообще говоря, зависящая от t. Разумеется, вместо ω1 (t,x) можно задать соответствующую характеристическую функцию

 2017-12-14
2017-12-14 479
479








