Определение средней долговечности при действии циклических напряжений со случайными амплитудами

Пусть процесс состоит из случайных симметричных циклов нагружений, характеризующихся максимальными напряжениями S в каждом. Используя гипотезу суммирования усталостных повреждений и уравнения кривых усталости N = N(S) при однородном режиме напряжений, когда известны эффективные периоды изменения напряжений 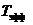и плотности вероятности 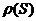максимальных значений процесса S(t), то средняя долговечность может быть определена по формуле Болотина В.В. [5]:

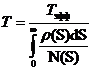
Для некоторых других представлений N = N(S) и 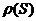процессов S(t) в таблице 3 [5] приводятся формулы вычисления средней долговечности. В этих формулах Г(х) – гамма-функция, 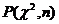- функция 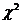- распределения Пирсона, протабулированная в различныхработах по курсу теории вероятности. Эффективный период 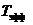выражают через спектральную плотность Ф(ω) процесса S(t) согласно формуле:

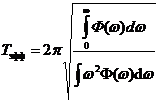
Строго говоря, эти формулы справедливы только для узкополосных стационарных эргодических случайных процессов. Для широкополосных случайных процессов они дают оценку снизу. В работе [10] даются формулы для нестационарных широкополосных случайных процессов. Вычисленная по этим формулам средняя долговечность является условной в том смысле, что она найдена при фиксированных характеристиках прочности. Учет разброса характеристик прочности рассмотрим в следующей лекции.