Применение теоремы Гаусса

1 2 3 4

а) Поле бесконечной заряженной плоскости (рис. 16.7)

Введем поверхностную плотность заряда

(

). Выбираем вспомогательную гауссову поверхность

, в данном случае в виде цилиндра, основания которого параллельны плоскости, а образующие перпендикулярны ей. Записываем теорему Гаусса

Рис. 16.7

Раскладываем интеграл по поверхности на 3 интеграла (по левому основанию, правому основанию и боковой поверхности): . Угол между и для левого основания равен нулю, значит , т.е. .

Аналогичный результат мы получим и для правого основания. Поток напряженности через боковую поверхность равен нулю (угол , ; силовые линии параллельны боковой поверхности, ее не пересекают).

Заряд, вырезаемый гауссовой цилиндрической поверхностью на заряженной плоскости, равен . Тогда, подставляя полученное выражение в теорему Гаусса, получим 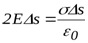, откуда напряженность поля заряженной плоскости равна

б) Поле плоского конденсатора.

Имеется две бесконечные заряженные плоскости, заряженные разноименно с поверхностной плотностью заряда

(рис. 16.8). Воспользуемся принципом суперпозиции. Напряженность поля в области I:

, где

- напряженности полей, создаваемых пластинами 1 и 2 соответственно. В проекции на ось X

Рис. 16.8

В области II .

В области III .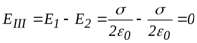

Таким образом, поле бесконечного плоского конденсатора сосредоточено внутри, между его пластинами, и равно

(Примечание: конденсатор можно считать бесконечным, если размеры пластин примерно на порядок больше расстояния между ними.)

в) Поле объемно-заряженного шара.

Пусть имеется равномерное скопление зарядов в виде шара (рис. 16.9) радиусом с объемной плотностью (). Поле шара обладает центральной симметрией. Записываем теорему Гаусса . Проведем внутри шара вспомогательную (гауссову) поверхность в форме сферы радиусом . Дальнейшие преобразования: . Напряженность по величине на одном и том же расстоянии от центра шара одинакова, поэтому, вынося за знак интеграла, получим:

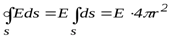, где 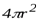- площадь гауссовой сферы.

Заряд, охватываемый гауссовой поверхностью, равен , где - объем шара.

В итоге, подставляя в теорему Гаусса, получаем , и поле внутри заряженной сферы
Рис. 16.9
Проведя аналогичные действия вне заряженной сферы, нетрудно получить График зависимости представлен на рис. 16.10.
Рис. 16.10