Лекция 18.
Электростатика в вакууме.
Электростатика устанавливает законы, определяющие поведение и взаимодействие неподвижных зарядов.
Современная физика оперирует понятием электромагнитного поля, рассматривая его, наряду с веществом, в качестве одного из видов материи. Этот вид материи – электромагнитное поле – обладает энергией, импульсом и может быть охарактеризован другими физическими свойствами. Именно посредством полей осуществляются электромагнитные взаимодействия тел.
Свойства электрического заряда.
Наряду с массой одной из основных характеристик частицы является её электрический заряд. Электрический заряд обладает свойствами:
1) Опытным путем установлено, что существуют как положительные, так и отрицательные электрические заряды. Этот экспериментальный факт называют дуализмом или двойственностью заряда.
Заряды одинакового знака отталкиваются, а разноименные заряды притягиваются.
2) Следующее утверждение, являющееся экспериментальным фактом, – это закон сохранения электрического заряда. Полный заряд (алгебраическая сумма зарядов) электрически изолированной системы никогда не меняется. Нарушения закона сохранения заряда не наблюдались.
|
|
|
3). Релятивистская инвариантность полного заряда:
алгебраическая сумма зарядов в изолированной системе не меняется при переходе от одной ИСО (инерциальной системы отсчета) к другой, независимо от скорости их относительного движения.
4). Квантование или дискретность заряда.
Полный заряд любого тела кратен элементарному заряду  . Опыты с макроскопическими телами позволяют установить дискретное изменение заряда лишь в тех случаях, когда избыточный заряд одного знака будет состоять лишь из небольшого числа элементарных. Такой случай реализуется вкапельном методе Милликена (описание опыта дается на лекции или см. в рекомендованной литературе), позволяющем достигнуть очень высокой точности в определении величины элементарного заряда.
. Опыты с макроскопическими телами позволяют установить дискретное изменение заряда лишь в тех случаях, когда избыточный заряд одного знака будет состоять лишь из небольшого числа элементарных. Такой случай реализуется вкапельном методе Милликена (описание опыта дается на лекции или см. в рекомендованной литературе), позволяющем достигнуть очень высокой точности в определении величины элементарного заряда.
Закон Кулона
 | Кулон (1785 г.) проводил опыты по измерению силы взаимодействия точечных зарядов (размеры заряженных тел значительно меньше расстояния между ними  , Рисунок 18.1) с помощью крутильных весов и открыл основной количественный закон электростатики. , Рисунок 18.1) с помощью крутильных весов и открыл основной количественный закон электростатики. |
| Рисунок 18.1. |
Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль прямой, соединяющей заряды.
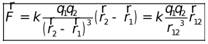 , ,  | (18.1) |
Выбор коэффициента 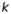 зависит от системы единиц. В системе СИ основные единицы: метр (м), килограмм (кг), секунда (с), Кельвин (К) и Ампер (А). При этом величина заряда и сила определяются независимо:
зависит от системы единиц. В системе СИ основные единицы: метр (м), килограмм (кг), секунда (с), Кельвин (К) и Ампер (А). При этом величина заряда и сила определяются независимо:
|
|
|
1 заряда (Кулон) = 1Кл = 1 А×1 с
Коэффициент  равен:
равен:
 |
где 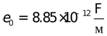 - диэлектрическая постоянная. Тогда значение коэффициента
- диэлектрическая постоянная. Тогда значение коэффициента  составляет
составляет  .
.
Напряженность электрического поля.
Взаимодействие между покоящимися зарядами осуществляется посредством электрического поля. Всякий электрический заряд определенным образом изменяет свойства окружающего пространства, т.е. создает в нем электрическое поле, которое может быть обнаружено по воздействию на «пробный» заряд q0. (Под пробным понимают такой заряд, который практически не изменяет электростатическое поле рассматриваемой системы зарядов).
Силовой характеристикой электрического поля служит векторная величина, называемая напряженностью электрического поля и определяемая как
 | (18.2) |
Напряженность поля, создаваемого точечным зарядом  в окружающем пространстве, определяется выражениями:
в окружающем пространстве, определяется выражениями:
 | (18.3) |
Однородным называется электрическое поле, напряженность которого во всех точках рассматриваемого пространства одинакова:
 | (18.4) |
Принцип суперпозиции (наложения) электрических полей вытекает из обобщения опытных фактов.
Опыт показывает, что сила, действующая на «пробный» заряд 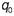 со стороны
со стороны  го заряда не изменяется в присутствии других зарядов:
го заряда не изменяется в присутствии других зарядов:
 | (18.5) |
Поэтому при наличии системы электрических зарядов полная сила, действующая на «пробный» заряд 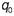 , будет равна векторной сумме сил, действующих на «пробный» заряд
, будет равна векторной сумме сил, действующих на «пробный» заряд 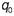 со стороны каждого заряда рассматриваемой системы:
со стороны каждого заряда рассматриваемой системы:
 | (18.6) |
Принцип суперпозиции Напряженность электрического поля, создаваемого всеми зарядами системы, в любой точке пространства определяется как векторная сумма напряженностей полей, создаваемых каждым отдельным зарядом:
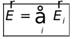 | (18.7) |
Если заряд распределен в пространстве непрерывно, то весь объем, содержащий заряд, разбивают на столь малые области, в пределах которых заряды можно считать точечными и равными по величине  , где
, где  - плотность заряда. Тогда электрическое поле, создаваемое таким зарядом находится как
- плотность заряда. Тогда электрическое поле, создаваемое таким зарядом находится как
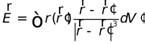 | (18.8) |
Закон Кулона. Напряженность электрического поля
Закон Кулона
 ,
,
где F — сила взаимодействия двухточечных зарядов Q1 и Q2; r — расстояние между зарядами; e — диэлектрическая проницаемость среды; e0 — электрическая постоянная:
 .
.
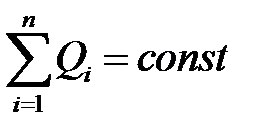 ,
,
где  — алгебраическаясуммазарядов,входящихв изолированную систему; n — число зарядов.
— алгебраическаясуммазарядов,входящихв изолированную систему; n — число зарядов.
· Напряженность электрического поля
 ,
,
где  — сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля.
— сила, действующая на точечный положительный заряд Q, помещенный в данную точку поля.
· Сила, действующая на точечный заряд Q, помещенный в электрическое поле
 .
.
· Поток вектора напряженности  электрического поля:
электрического поля:
а) через произвольную поверхность S, помещенную в неоднородное поле,
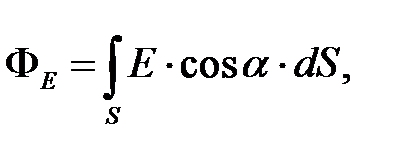 или
или 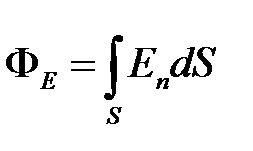 ,
,
где a — угол между вектором напряженности  и нормалью
и нормалью  к элементу поверхности;
к элементу поверхности;  — площадь элемента поверхности; En — проекция вектора напряженности на нормаль;
— площадь элемента поверхности; En — проекция вектора напряженности на нормаль;
б) через плоскую поверхность, помещенную в однородное электрическое поле
Ф E=Е∙S∙ cosa.
· Поток вектора напряженности  через замкнутую поверхность
через замкнутую поверхность
 ,
,
где интегрирование ведется по всей поверхности.
· Теорема Остроградского — Гаусса. Поток вектора напряженности  через любую замкнутую поверхность, охватывающую заряды Ql, Q2,..., Qn
через любую замкнутую поверхность, охватывающую заряды Ql, Q2,..., Qn
 ,
,
где  — алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; п — число зарядов.
— алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; п — число зарядов.
· Напряженность электрического поля, создаваемого точечным зарядом Q на расстоянии r от заряда
 .
.
Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд Q, на расстоянии r от центра сферы:
а) внутри сферы (r<R)E =0;
б) на поверхности сферы (r = R)  ;
;
в) вне сферы (r>R)  .
.
· Принцип суперпозиции (наложения) электрических полей, согласно которому напряженность  результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:
результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:
|
|
|
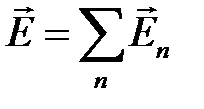 .
.
В случае двух электрических полей с напряженностями  и
и  модуль вектора напряженности
модуль вектора напряженности
 ,
,
где a — угол между векторами  и
и  .
.
· Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) нарасстоянии r от ее оси
 ,
,
где t — линейная плотность заряда.
Линейная плотность заряда распределенного по нити (цилиндру) есть величина, равная заряду, приходящемуся на единицу ее длины:

· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

где s — поверхностная плотность заряда.
Поверхностная плотность заряда распределенного по поверхности есть величина, равная заряду, приходящемуся на единицу этой поверхности:
 .
.
· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью  заряда (поле плоского конденсатора)
заряда (поле плоского конденсатора)
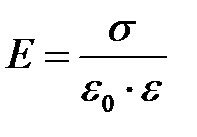 .
.
Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
· Электрическое смещение  связано с напряженностью
связано с напряженностью  электрического поля соотношением
электрического поля соотношением
 .
.
Это соотношение справедливо только дляизотропных диэлектриков.
· Циркуляция вектора напряженности электрического поля есть величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль замкнутого контура. Циркуляция выражается интегралом по замкнутому контуру  , где El – проекция вектора напряженности
, где El – проекция вектора напряженности  в данной точке контура на направление касательной к контуру в той же точке.
в данной точке контура на направление касательной к контуру в той же точке.
В случае электростатического поля циркуляция вектора напряженности равна нулю:
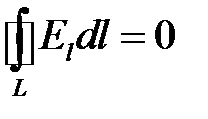 .
.
Теоретический материал Электрические заряды. Элементарный электрический заряд. Проводники и диэлектрики. Закон сохранения электрического заряда. Взаимодействие электрически заряженных тел. Электроскоп. Точечный заряд. Закон Кулона. Электрическое поле. Напряженность электрического поля. Линии напряженности электрического поля (силовые линии). Однородное электрическое поле. Напряженность электростатического поля точечного заряда. Принцип суперпозиции полей. Теорема Гаусса. Поле равномерно заряженной плоскости, сферы и шара. Понятие электрический заряд - основополагающее первичное понятие, несводимое к более простым, элементарным понятиям. Взаимодействия между заряженными частицами называются электромагнитными, их интенсивность пропорциональна величине электрического заряда. Существуют заряды двух противоположных знаков. Положительный заряд возникает на стекле, натертом кожей, отрицательный - на янтаре, натертом шерстью. Частицы, обладающие одноименными зарядами, отталкиваются, разноименными - притягиваются. Частицы могут не обладать зарядом, но не бывает заряда вне частиц. Существует минимальный заряд, называемый элементарным, которым обладают заряженные элементарные частицы. Отделить часть заряда, например, у электрона или протона, невозможно. Заряд протона считается положительным, электрона - отрицательным (электрон и протон существуют в свободном состоянии неограниченно долго). Тело называется наэлектризованным, если нарушена его электрическая нейтральность. Электрический заряд любого тела равен целому числу элементарных зарядов. Проводниками называются вещества, в которых может происходить перемещение свободных зарядов - металлы, растворы электролитов, ионизованные газы. Диэлектриками называются вещества, не проводящие электрический ток (свободные заряды отсутствуют) - стекло, фарфор, керосин, и т.д. Во всех известных явлениях и экспериментах алгебраическая сумма зарядов всех частиц замкнутой системы сохраняется - закон сохранения электрического заряда. Кулону экспериментально (с помощью крутильных весов) удалось установить закон взаимодействия неподвижных заряженных тел - закон Кулона: сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.  , ,  = 9·109 Н·м2/Кл2. Силы кулоновского взаимодействия двух неподвижных точечных зарядов направлены вдоль прямой, соединяющей эти тела, т.е. являются центральными силами. Заряды называются точечными, если они расположены на телах, размеры которых существенно меньше расстояния между ними. Единица заряда в системе СИ - кулон (Кл). 1 Кл - заряд, проходящий за одну секунду через поперечное сечение проводника при силе тока в 1 А. Заряд электрона e = − 1,6·10−19 Кл. Электрические заряды не действуют друг на друга непосредственно; каждый заряд создает в окружающем пространстве электрическое поле, действующее на другие заряды (теория близкодействия, Фарадей). Поле материально, оно существует независимо от нас и обладает определенными свойствами, главное из которых - действие со стороны поля на электрические заряды с некоторой силой. Из закона Кулона: при взаимодействии точечных зарядов отношение силы, действующей на заряд в данной точке поля, к величине этого заряда есть постоянная величина - силовая характеристика поля. Напряженностью электрического поля называется векторная физическая величина, равная отношению силы, с которой поле действует на пробный точечный заряд, к величине этого заряда = 9·109 Н·м2/Кл2. Силы кулоновского взаимодействия двух неподвижных точечных зарядов направлены вдоль прямой, соединяющей эти тела, т.е. являются центральными силами. Заряды называются точечными, если они расположены на телах, размеры которых существенно меньше расстояния между ними. Единица заряда в системе СИ - кулон (Кл). 1 Кл - заряд, проходящий за одну секунду через поперечное сечение проводника при силе тока в 1 А. Заряд электрона e = − 1,6·10−19 Кл. Электрические заряды не действуют друг на друга непосредственно; каждый заряд создает в окружающем пространстве электрическое поле, действующее на другие заряды (теория близкодействия, Фарадей). Поле материально, оно существует независимо от нас и обладает определенными свойствами, главное из которых - действие со стороны поля на электрические заряды с некоторой силой. Из закона Кулона: при взаимодействии точечных зарядов отношение силы, действующей на заряд в данной точке поля, к величине этого заряда есть постоянная величина - силовая характеристика поля. Напряженностью электрического поля называется векторная физическая величина, равная отношению силы, с которой поле действует на пробный точечный заряд, к величине этого заряда 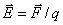 . Однородное электрическое поле - напряженность поля одинакова во всех точках пространства. Силовые линии электростатического поля, или линии напряженности (графический способ описания поля), - непрерывные линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности, а их густота пропорциональна величине напряженности. Линии напряженности электростатического поля не пересекаются и не обрываются: они начинаются на положительных зарядах, кончаются на отрицательных, либо уходят в бесконечность. Принцип суперпозиции полей: если в данной точке пространства несколько заряженных частиц создают поля, напряженности которых равны . Однородное электрическое поле - напряженность поля одинакова во всех точках пространства. Силовые линии электростатического поля, или линии напряженности (графический способ описания поля), - непрерывные линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности, а их густота пропорциональна величине напряженности. Линии напряженности электростатического поля не пересекаются и не обрываются: они начинаются на положительных зарядах, кончаются на отрицательных, либо уходят в бесконечность. Принцип суперпозиции полей: если в данной точке пространства несколько заряженных частиц создают поля, напряженности которых равны  , , 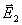 , ,  ,..., то результирующая напряженность поля в этой точке ,..., то результирующая напряженность поля в этой точке  . Теорема Гауссасвязывает число силовых линий, исходящих из замкнутой поверхности N с суммарным зарядом . Теорема Гауссасвязывает число силовых линий, исходящих из замкнутой поверхности N с суммарным зарядом  , находящимся внутри этой поверхности , находящимся внутри этой поверхности  . Напряженность поля точечного заряда: . Напряженность поля точечного заряда: 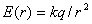 . . 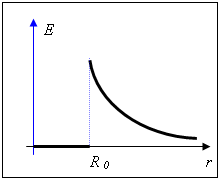 Напряженность поля равномерно заряженной сферы Напряженность поля равномерно заряженной сферы  Напряженность поля равномерно заряженной плоскости Напряженность поля равномерно заряженной плоскости  , где , где  - поверхностная плотность заряда. - поверхностная плотность заряда. |


|
|
|
 2017-12-14
2017-12-14 5112
5112