2017-12-14
688
Сформулированные Максвеллом уравнения классической электродинамики связывают электрическое и магнитное поле с движением заряженных частиц. Эти уравнения почти симметричны относительно электричества и магнетизма. Они могут быть сделаны полностью симметричными, если в дополнение к электрическому заряду и току ввести некий магнитный заряд с объемной плотностью распределения z m и магнитный ток с плотностью j m:
| Название | Без магнитных монополей | С магнитными монополями |
| Теорема Гаусса: | div D = 
| 
|
| Магнитный закон Гаусса | 
| 
|
| Закон индукции Фарадея: | rot E = 
| 
|
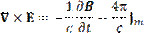
| Закон Ампера (с током смещения): | 
| 
|
Уравнения из правой колонки переходят в классические уравнения при подстановке 
и 
, то есть если в рассматриваемой области пространства отсутствуют магнитные заряды.
Поль Дир а к создал квантовую теорию взаимодействия электрического заряда e с магнитным зарядом g [ qm ], которая применима при условии:
, где n — целое число. Таким образом, магнитный заряд частицы должен быть кратен элементарному магнитному заряду 
, где e — элементарный электрический заряд. В используемой системе единиц e и g имеют одинаковую размерность, причём заряд e фиксирован соотношением
[или e 2/ ħc?]
– известная из атомной физики постоянная тонкой структуры.
