Основное уравнение гидростатики. Рассмотрим силы, действующие в покоящейся жидкости, и выведем уравнение для определения величины гидростатического давления в любой точке жидкости

Рассмотрим силы, действующие в покоящейся жидкости, и выведем уравнение для определения величины гидростатического давления в любой точке жидкости. Силы, действующие в жидкости, можно разделить на две группы – поверхностные и массовые.

Выделим в жидкости, находящейся в равновесии, элементарный параллелепипед с ребрами dx, dy, dz, параллельными соответствующим осям произвольно расположенной в пространстве прямоугольной системы координат (рис. 2 –1). Отбросим мысленно окружающую параллелепипед жидкость, заменив ее действие на грани соответствующими поверхностными силами – силами гидростатического давления.

Согласно первому свойству гидростатического давления эти силы будут нормальны к поверхностям соответствующих граней и направлены внутрь параллелепипеда. Допустим, на левую грань параллелепипеда площадью dx.dy действует гидростатическое давление равное p_x, причем величина его будет зависеть от положения границы в пространстве, занятом жидкостью, т.е. p_x = f(x, y, z).

Определим гидростатическое давление на противоположную грань. Очевидно, если мы будем переходить вдоль оси Ox от левой грани к противоположной, то давление p_x, будет плавно и непрерывно изменяться. Изменение давления p_x на единицу длины вдоль оси Ox будет равно частной производной , так как приращение функции p_x = f(x, y, z) происходит за счет изменения только одной независимой переменной - координаты x, при y=const и z=const. Приращение давления p_x на длине ребра dx будет , а давление на противоположную грань

 

 

Аналогично можно получить изображенные на рис. 2 – 1 величины гидростатических давлений на все попарно противоположные грани параллелепипеда.

Умножив гидростатические давления на площади соответствующих граней, получим поверхностные силы, действующие на грани параллелепипеда со стороны окружающей жидкости. Например, на левую правую грани будут действовать нормальные поверхностные силы давления равные, соответственно

и .

Определим массовые силы, действующие на выделенный параллелепипед. На каждую единицу массы, заключенную в объеме параллелепипеда, действует единичная массовая сила. Обозначим проекции единичных массовых сил на оси координат Ox, Oy, Oz соответственно через X, Y, Z. В объеме параллелепипеда заключена масса жидкости, равная ее плотности r, умноженной на объем параллелепипеда dx.dy.dz, т.е. r.dx.dy.dz. Поэтому проекции на координатные оси массовых сил, действующих на всю массу жидкости в объеме параллелепипеда, будут, соответственно, равны

.

Так как параллелепипед находится в равновесии, то суммы проекций всех сил, действующих на него, на координатные оси должны быть равны нулю. Уравнение равновесия параллелепипеда в направлении оси Ox будет иметь вид

.

Приведя подобные члены, получим:

.

Поделим уравнение на r.dx.dy.dz (массу жидкости в объеме параллелепипеда) и тем самым отнесем его к единице массы жидкости:

.

Составляя уравнения равновесия в направлении осей Oy и Oz, аналогично можно получить:

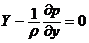и .

Стягивая параллелепипед к точке, т.е. устремляя dx, dy, dz к нулю, согласно второму свойству гидростатического давления (1 – 2), получим окончательно:

 

(2 – 1)

Выражения (2 – 1) представляют систему дифференциальных уравнений гидростатики – уравнений Эйлера. Уравнения Эйлера являются общими условиями равновесия жидкости. Они устанавливают связь между массовыми силами, давлением и координатами в каждой точке покоящейся жидкости.

Проинтегрируем уравнения Эйлера для частного случая, когда жидкость находится в равновесии под действием только силы тяжести (другие массовые силы отсутствуют).

Предварительно преобразуем уравнения. Умножим каждое из уравнений Эйлера, соответственно, на dx, dy, dz и сложим полученные выражения. Будем иметь:

.

В правой части уравнения в скобках имеем полный дифференциал гидростатического давления

,

так как

.

Тогда

. (2 - 2)

Перед интегрированием уравнения (2 – 2) определим для рассматриваемого случая проекции X, Y, Z массовой силы – силы тяжести на оси координат.

Выберем систему прямоугольных координат, удобную для решения практических задач (рис. 2 – 2). Расположим начало и оси Ox и Oy на горизонтальной свободной поверхности жидкости, а ось Oz направим вертикально вниз. При этом проекции силы тяжести, действующей на единицу массы, на оси координат будут равны

 

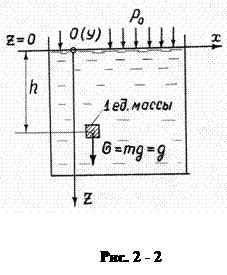
Подставляя эти величины в (2 – 2), получим

или .

Интегрируя, будем иметь

.

Постоянную интегрирования C определим из условия на свободной поверхности жидкости. При z=0, p=p_o, откуда

C = p_o,

где: p_o – внешнее давление на единицу свободной поверхности жидкости (в открытом сосуде – атмосферное давление).

Получаем:

.

Вводя вместо z обычно применяемое в гидравлике понятие глубины h погружения данной точки под уровнем свободной поверхности, окончательно будем иметь

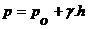. (2 – 3)

Выражение (2 – 3) называется основным уравнением гидростатического давления. Оно позволяет найти величину полного (абсолютного) гидростатического давления в любой точке жидкости при действии на нее силы тяжести. Как видно из (2 – 3), полное гидростатическое давление складывается из двух частей:

- давления p_o на свободной поверхности жидкости и

- давления g.h, обусловленного весом вышележащего столба жидкости (весовая часть гидростатического давления), которое зависит от удельного веса жидкости.

Из основного уравнения гидростатического давления вытекают два следствия – так называемое третье свойство гидростатического давления и закон Паскаля. Возьмем две произвольные точки в жидкости, расположенные на разной глубине под уровнем свободной поверхности (рис. 2 – 3). Согласно (2 – 3) гидростатические давления в них будут:

(2 – 4)

(2 – 5)

Сравнивая (2 – 4) и (2 – 5), видим, что при одинаковом давлении на свободной поверхности жидкости величина гидростатического давления зависит только от глубины погружения данной точки под уровень свободной поверхности. Это и есть третье свойство гидростатического давления.