Скорость равномерного осаждения или всплывания твердого тела в жидкости легко определяется из уравнения (18.26), которое для участка равномерного движения упрощается в связи с равенством нулю ускорения ( ). Рассмотрим случай осаждения сферической твердой частицы в вязкой жидкости (рис. 18.18).
). Рассмотрим случай осаждения сферической твердой частицы в вязкой жидкости (рис. 18.18).
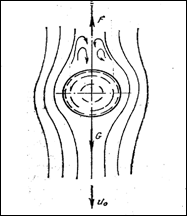
Рис 18.18. Осаждение твердой сферы в вязкой жидкости
Вес частицы с учетом силы взвешивания
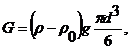 (18.27)
(18.27)
где ρ и ρ0 - соответственно плотности твердой частицы и жидкости; d - диаметр частицы.
Очевидно, что при всплывании твердой частицы в уравнении (18.27) следует записать первый сомножитель в виде ρ0-ρ. Сила лобового сопротивления в соответствии с формулой (18.22) определится в виде
 (18.28)
(18.28)
где u 0 - скорость равномерного движения твердой частицы.
Приравнивая правые части выражений (18.27) и (18.28), и решая полученное уравнение относительно скорости u 0 получим
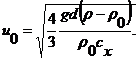 (18.29)
(18.29)
Уравнение (18.29) при известном значении с xпозволяет определить гидравлическую крупность или скорость витания в зависимости от конкретных условий решаемой задачи. Недостатком этого уравнения является неопределенность коэффициента лобового сопротивления с x, зависящего, как известно, от числа Рейнольдса, которое вычисляется по скорости осаждения или всплывания u 0.
При движении весьма малых частиц (Re<l) уравнение (18.29) в соответствии с равенством  приобретает вид уравнения Стокса
приобретает вид уравнения Стокса
 (18.30)
(18.30)
При расчете скорости равномерного движения частиц, имеющих форму, отличную от сферической, вводится понятие диаметра, эквивалентного по объему, или диаметра, эквивалентного по площади поверхности шара.
В этом случае расчет усложняется, однако и здесь для первого приближения можно использовать уравнения (17.29) и (17.30), подставляя в них значения эквивалентного диаметра, например по объему, и соответствующий форме частицы коэффициент лобового сопротивления. За пределами закона Стокса уравнение (17.29) обычно решается подбором или графически.
Запишем уравнение динамического равновесия (17.26) для случая равномерного осаждения твердой сферической частицы в безразмерном виде
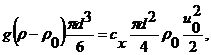 (18.31)
(18.31)
или
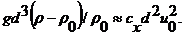 (18.32)
(18.32)
Разделим уравнение (18.32) на v 2
 (18.33)
(18.33)
В левой части уравнения (18.33) записан безразмерный комплекс  , называемый критерием Архимеда, в правой части - произведение значения коэффициента лобового сопротивления c xна квадрат значения критерия Рейнольдса. Так как коэффициент лобового сопротивления для частиц определенной формы зависит только от числа Рейнольдса
, называемый критерием Архимеда, в правой части - произведение значения коэффициента лобового сопротивления c xна квадрат значения критерия Рейнольдса. Так как коэффициент лобового сопротивления для частиц определенной формы зависит только от числа Рейнольдса 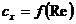 , уравнение равномерного осаждения (всплывания) твердых частиц в жидкости можно представить в виде
, уравнение равномерного осаждения (всплывания) твердых частиц в жидкости можно представить в виде
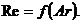 (18.34)
(18.34)
С помощью графика этой зависимости (рис. 18.19) гидравлическая крупность сферических частиц определяется без затруднений, так как критерий Архимеда для заданного диаметра сферы однозначно определяет значение критерия Рейнольдса, из которого и находится гидравлическая крупность. Экспериментальные графики, аналогичные графику зависимости (18.34), могут быть легко построены для частиц любой формы.
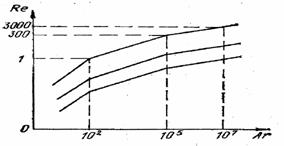
Рис. 18.19. Зависимость 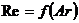 равномерного осаждения (всплывания) твердой сферы в вязкой жидкости
равномерного осаждения (всплывания) твердой сферы в вязкой жидкости
Графическая зависимость 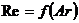 аппроксимируется приближенными формулами, которые имеют хорошее подтверждение в опытах не только для равномерного осаждения (всплывания) одиночных частиц, но и для стесненного (массового) их осаждения:
аппроксимируется приближенными формулами, которые имеют хорошее подтверждение в опытах не только для равномерного осаждения (всплывания) одиночных частиц, но и для стесненного (массового) их осаждения:
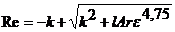 (18.35)
(18.35)
или
 (18.36)
(18.36)
где k и  - безразмерные экспериментальные постоянные, зависящие от формы частиц (для сферических частиц
- безразмерные экспериментальные постоянные, зависящие от формы частиц (для сферических частиц 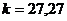 ,
,  );
); 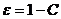 (здесь
(здесь 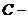 объемная концентрация твердых частиц).
объемная концентрация твердых частиц).
Обобщенное уравнение (18.35) справедливо для любого гидравлического режима осаждения, уравнение (18.36) только для переходного режима при  .
.
 2017-12-14
2017-12-14 1545
1545








