Задача 1.
1. Найпростішим методом обчислення визначеного інтеграла є формула Ньютона-Лейбніца:
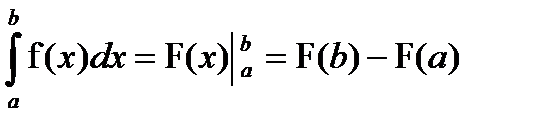
де F (х) – будь-яка первісна від функції f (х).
2. Метод заміни змінної використовують тоді, коли можна вибрати таку функцію x = g (t), що після підстановки підінтегральна функція стане простішою. Якщо при обчисленні інтеграла 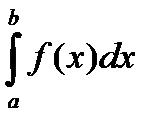 робиться підстановка x = g (t), то формула заміни змінної має вигляд:
робиться підстановка x = g (t), то формула заміни змінної має вигляд:
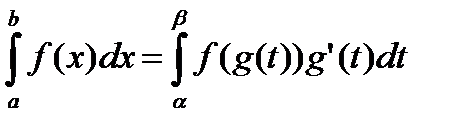 ,
,
де α, β – нові межі інтегрування, що знаходятьіз рівностей a = g (α), b = g (β).
3. При обчисленні визначеного інтеграла необхідно обов’язково перерахувати межі інтегрування. Повертатися до старої змінної не треба.
Задача 2.
1. Формула інтегрування частинами для визначеного інтеграла має вигляд:
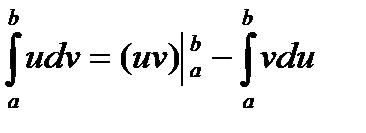 .
.
2. Множники u (х) і dv обираються так само, як в невизначеному інтегралі.
Задача 3.
1. Нехай функція f (х) інтегрована на будь-якому відрізку [ a; b ], тоді інтеграли
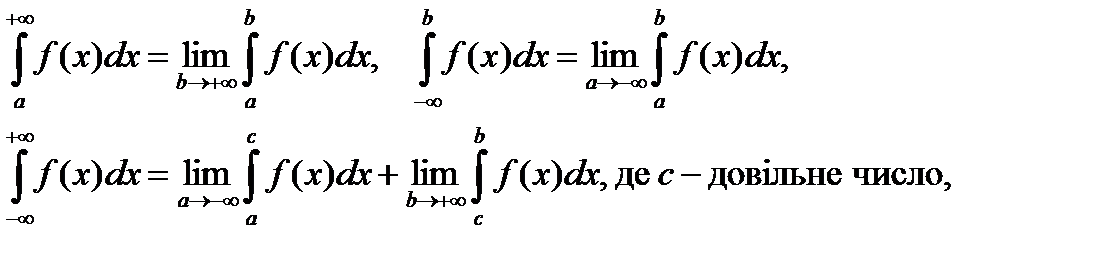
називаються невласними інтегралами першого роду.
2. Якщо границі в правих частинах формул скінчені, то інтеграли називаються збіжними. Якщо ці границі не існують або дорівнюють нескінченості, то інтеграли є розбіжними.
Задача 4.
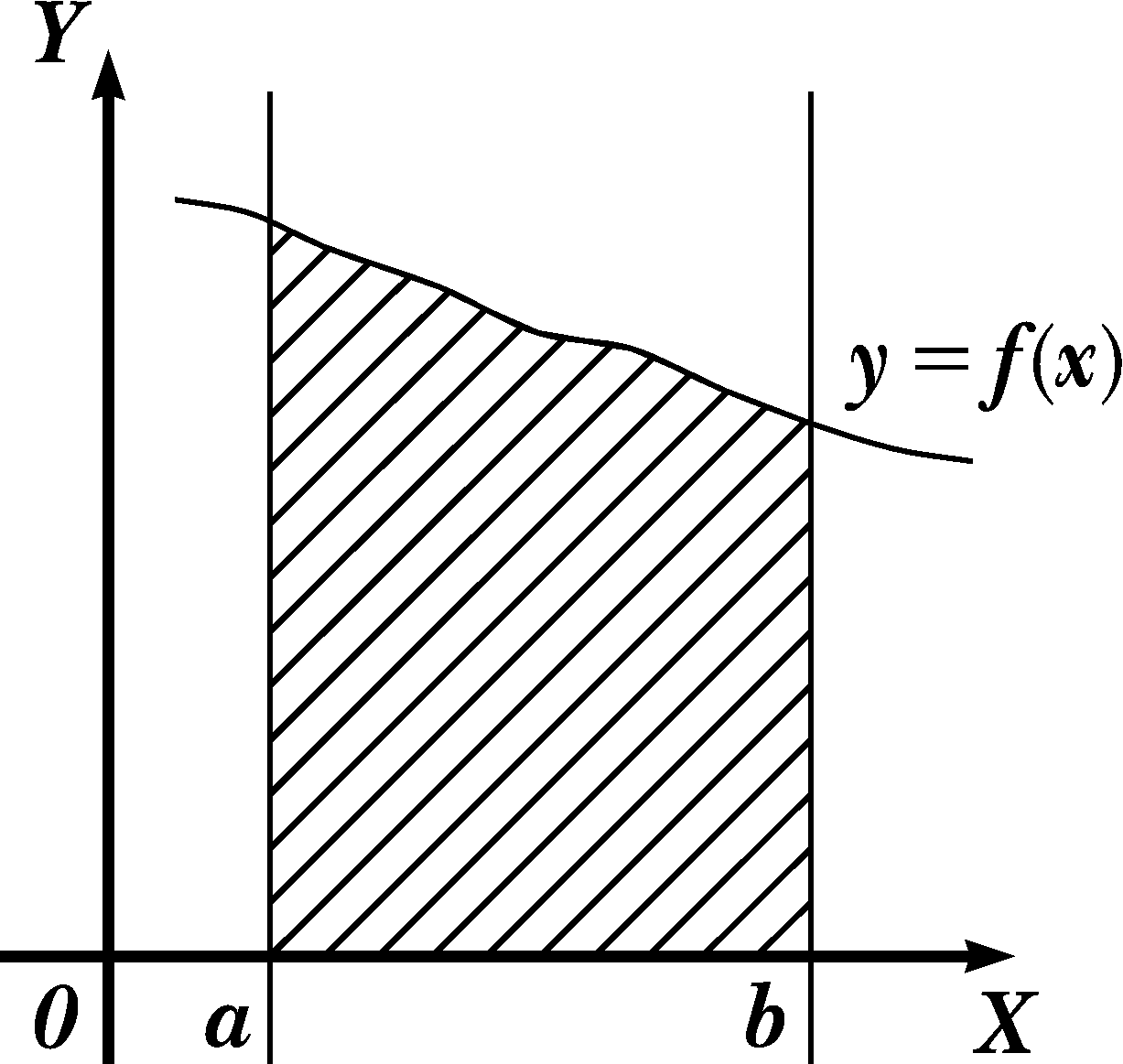
1. Площа криволінійної трапеції, обмеженої графіком функції у = f (х) ³ 0, віссю О х і прямими х = а, х = b (рис. 1 а), обчислюється за формулою:
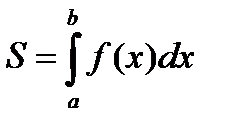 .
.
 а
а
|  б
б
|
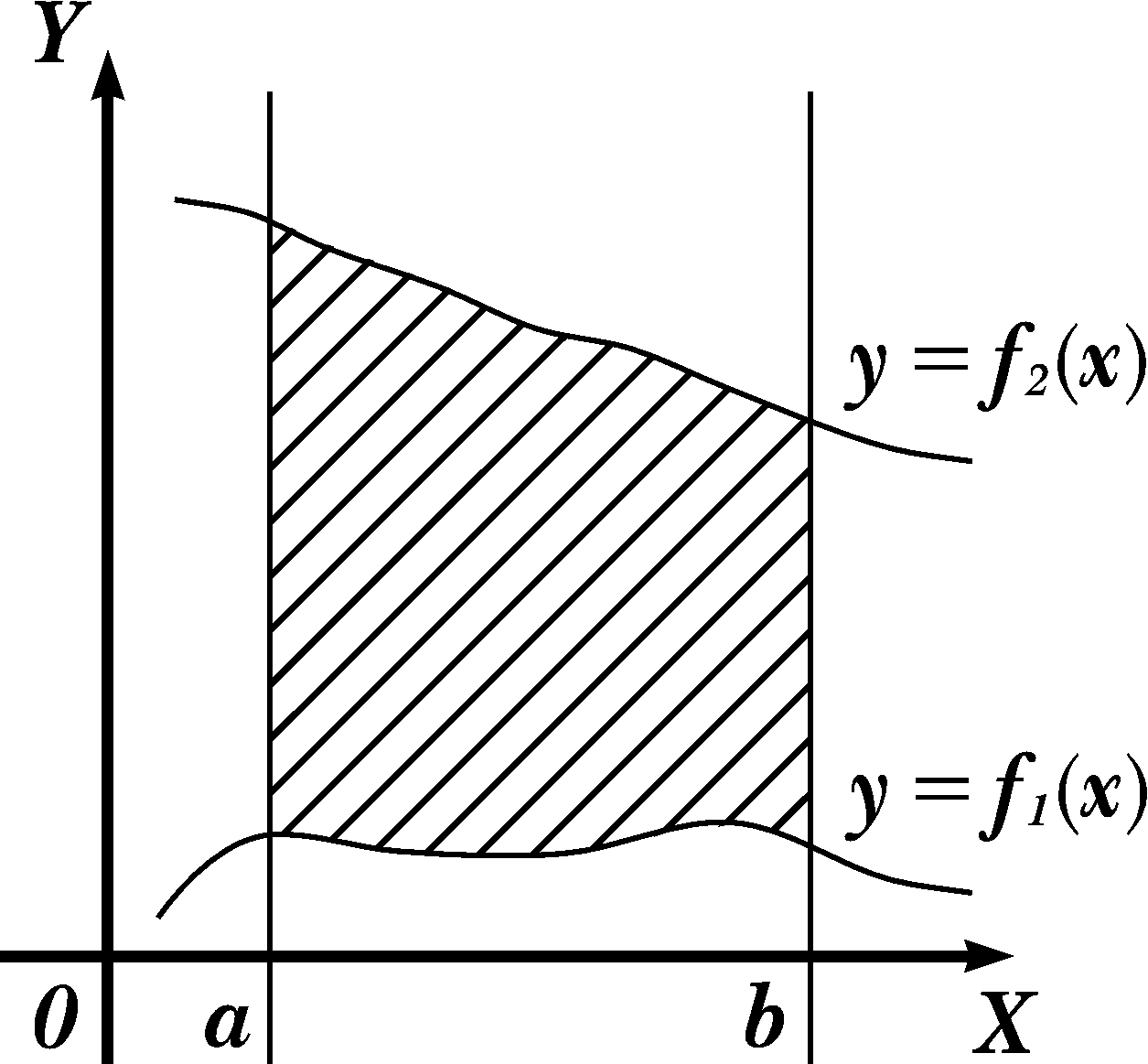
Рис. 1.
2. Якщо f (х) < 0 на [ a; b ], то 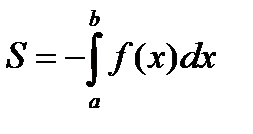 .
.
3. Якщо фігура обмежена зверху графіком функції у = f 2(х), знизу – у = f 1(х), зліва і справа прямими х = а, х = b відповідно (рис. 1 б), то її площа обчислюється за формулою:
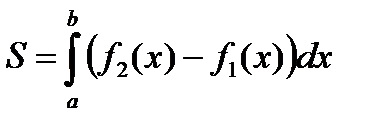 .
.
4. Якщо фігура обмежена зверху лінією, що задана параметричними рівняннями х = х (t), у = у (t)> 0, t  [ t 1; t 2], знизу – віссю О х, зліва і справа –прямими х = а, х = b, то її площа дорівнює:
[ t 1; t 2], знизу – віссю О х, зліва і справа –прямими х = а, х = b, то її площа дорівнює:
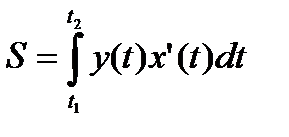 ,
,
причому х (t 1) = а, х (t 2) = b.
Задача 5.
1. Нехай криволінійна трапеція (рис. 1 а) обертається навколо осі О х. Тоді об’єм тіла обертання дорівнює:
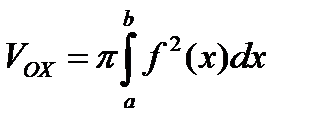 .
.
2. Об’єм тіла, що утворене обертанням навколо осі О у фігури, яка обмежена лініями у = с, у = d, х = 0, х = g(у), обчислюється за формулою:
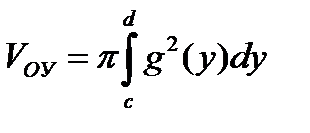 .
.
3. Якщолінія, що обмежує криволінійну трапецію, задана параметричними рівняннями х = х (t), у = у (t), t 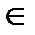 [ t 1; t 2], то об’єм тіла обертання навколо осі О х обчислюється за формулою:
[ t 1; t 2], то об’єм тіла обертання навколо осі О х обчислюється за формулою:
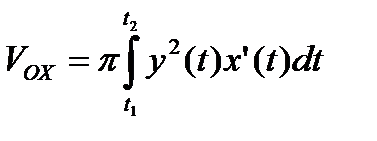
 2017-12-14
2017-12-14 466
466








