Первое уравнение Максвелла

За исходное выражение возьмем первое уравнение Максвелла в интегральной форме (1.6). Применим к его левой части теорему Стокса:

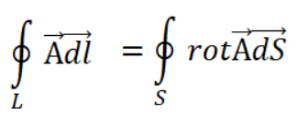
Получим следующее уравнение:

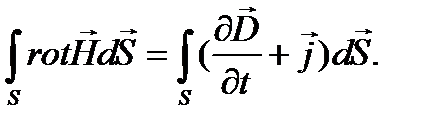
Поскольку интегрирование в обеих частях уравнения идетпо одной и той же произвольной поверхности, то из равенства интегралов следует равенство подынтегральных функций, т.е.

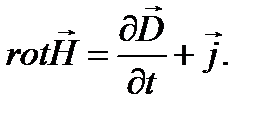(1.10)

Физический смысл первого уравнения Максвелла в дифференциальной (1.10) и интегральной (1.6) формах формулируется так: магнитное поле создается как изменяющимся во времени электрическим полем (током смещения), так и движущимися зарядами (током проводимости).

При этом направление вектора 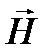связано с направлением плотностей тока смещения 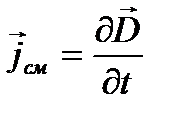(рис.1.3,а) и проводимости j (рис. 1.3,б) правилом правого винта.

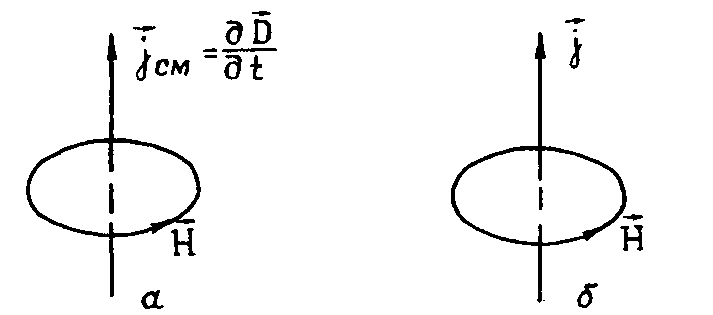
Рисунок 1.3 – Связь векторов 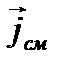, 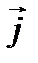и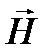

Направление тока смещения, в свою очередь, определяется направлением вектора электрической индукции 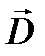и характеромего изменения, т.е. знаком производной 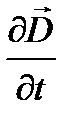. Так, при увеличении интенсивности электрического поля вектор 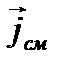совпадает с направлением вектора 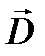(рис. 1. 4,а). При уменьшении интенсивности электрического поля вектор 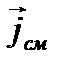направлен противоположно вектору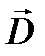
(рис.1.4,б).

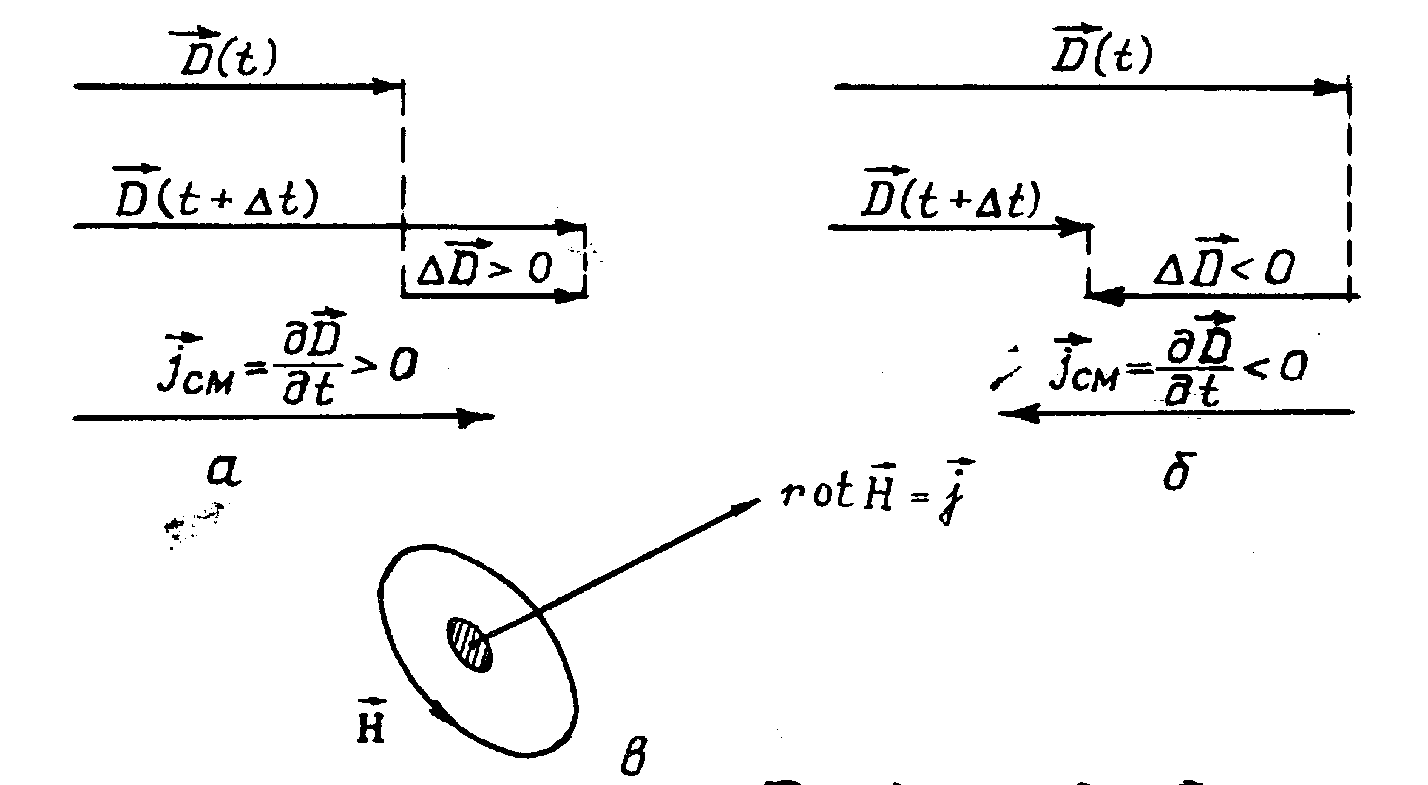
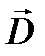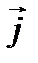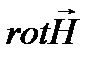Рисунок 1.4 – Связь векторов и , и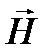

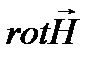определяется как мера завихрения магнитного поля, т.е. максимальная его циркуляция в точке, и является векторной величиной. Вектор совпадает с направлением вектора плотности тока, следовательно, 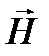и 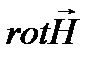связаны правилом правого винта (рис. 1.4,в).

Важность первого закона электродинамики состоит в том, что он утверждает неизбежность возбуждения магнитного поля переменным электрическим полем, которое может существовать в диэлектрике и даже в вакууме.