Для получения дифференциальной формы записи этого уравнения Максвелла применим к левой части (1.8) теорему Остроградского – Гаусса
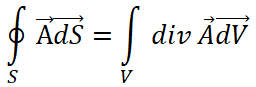
Тогда 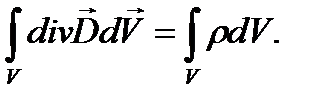
Так как интегрирование в обеих частях выражения идет по одному и тому же произвольному объему V,то из равенства интегралов следует равенство подынтегральных функций
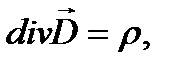 (1.12)
(1.12)
где 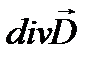 – дивергенция (расходимость) силовых линий электрического смещения. Она является мерой объемной плотности заряда.
– дивергенция (расходимость) силовых линий электрического смещения. Она является мерой объемной плотности заряда.
Если в некоторой области dV находится положительный заряд (ρ >0), то 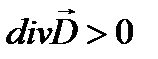 – силовые линии
– силовые линии 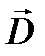 выходят из этой области (рис. 1.5,а). Если заряд в области отрицательный ρ <0, то
выходят из этой области (рис. 1.5,а). Если заряд в области отрицательный ρ <0, то 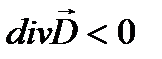 – силовые линии
– силовые линии 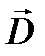 сходятся в эту область (рис. 1.5,б). Если же заряда в области нет, то
сходятся в эту область (рис. 1.5,б). Если же заряда в области нет, то 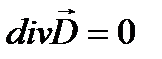 и силовые линии пронизывают эту область. При этом количество силовых линий, входящих в область, равно количеству линий, выходящих из нее (рис.1.5, в).
и силовые линии пронизывают эту область. При этом количество силовых линий, входящих в область, равно количеству линий, выходящих из нее (рис.1.5, в).
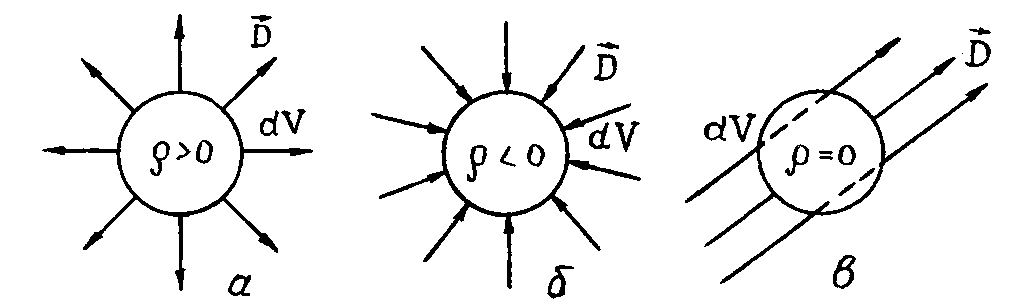
Рисунок 1.5 – К понятию дивергенции вектора 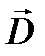
Физический смысл третьего уравнения Максвелла: электрические заряды возбуждают электрическое поле, причем положительные заряды являются истоками, а отрицательные – стоками электрического поля 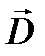 ,
,  .
.
 2017-12-14
2017-12-14 990
990








