Применив теорему Остроградского – Гаусса к (1.9), получим дифференциальную форму записичетвертого уравнения Максвелла
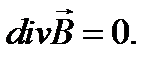 (1.13)
(1.13)
Физический смысл четвертого закона состоит в том, что магнитные силовые линии 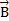 нигде не начинаются и не кончаются: они или замкнуты или уходят в бесконечность.
нигде не начинаются и не кончаются: они или замкнуты или уходят в бесконечность.
Уравнения Максвелла можно записать с помощью дифференциального оператора набла  :
:
1.  3.
3. 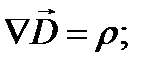
(1.14)
2. 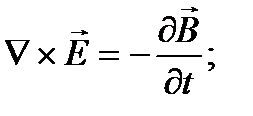 4.
4. 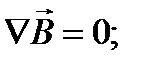
Для прямоугольной системы координат дифференциальный оператор набла  имеет вид:
имеет вид:
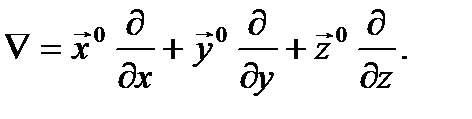
С помощью электромагнитного поля, распространяющегося в пространстве в виде электромагнитных волн, можно передавать информацию. Тогда комплексные векторы  ,
, 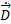 ,
, 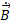 ,
, 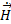 должны меняться во времени в соответствии с передаваемым сигналом, который, зачастую, меняется во времени по гармоническому закону. Эта ситуация характерна для радиоэлектронных средств, работающих с гармоническими монохроматическими сигналами. Тогда применительно к гармоническим электромагнитным полям (случайкомплексных амплитуд), учитывая, что
должны меняться во времени в соответствии с передаваемым сигналом, который, зачастую, меняется во времени по гармоническому закону. Эта ситуация характерна для радиоэлектронных средств, работающих с гармоническими монохроматическими сигналами. Тогда применительно к гармоническим электромагнитным полям (случайкомплексных амплитуд), учитывая, что 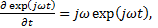 получим уравнения Максвелла для комплексных амплитуд поля
получим уравнения Максвелла для комплексных амплитуд поля
rot 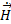 = jω
= jω  +
+ 
rot  = -jω
= -jω 
div  =
= 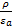 (1.15)
(1.15)
div 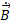 = 0.
= 0.
С математической точки зрения уравнения Максвелла представляют собой систему дифференциальных уравнений, куда входят пять векторных и одна скалярная функции:  ,
, 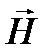 ,
, 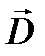 ,
,  ,
, 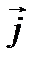 и ρ.
и ρ.
Для их отыскания необходимо иметь шесть независимых уравнений. Можно показать, что третье уравнение Максвелла является следствием второго. Тогда система уравнений Максвелла содержит лишь три независимых уравнения (два векторных и одно скалярное), т.е. является неполной. Поэтому ее дополняют тремя материальными уравнениями (1.4).
В заключение отметим, что каждое векторное уравнение можно представить в виде трех скалярных уравнений.
 2017-12-14
2017-12-14 1959
1959
