Дальняя (волновая) зона или зона Фраунгофера

Для дальней зоны kr>>1 или r>>λ. Поэтому 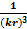<< << 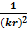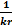. Пренебрежем слагаемым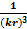и и 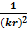по сравнению с 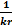и тогда выражения (2.1), (2.2), (2.3) примут вид:

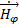(r, θ, t) = 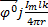sinθ ; (2.8)

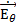(r, θ, t) = 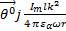sinθ , (2.9)

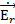(r, θ, t) = 0.

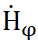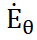Из выражений (2.8) и (2.9) следует, что и синфазны.Это возможно, если k и 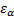–вещественны.

Отношение 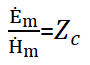называется волновым (характеристическим) сопротивлением среды. Проверим размерность этого отношения: 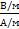= [Oм].

Определим волновое сопротивление среды, где распространяются электромагнитные волны

= = = =

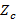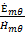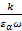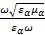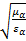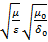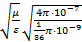= = = = 120 π 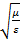[Ом] (2.10)

Если μ = 1 и ε = 1, то получим характеристическое сопротивление вакуума (воздуха):

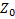= 120 π 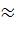377 [Ом]. (2.11)

Амплитуду напряженности электрического поля можно
представить:

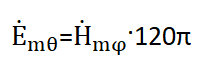
С учетом этого соотношения и, подставив k = 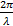, преобразуем выражения (2.8) и (2.9):

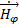(r, θ, t) = 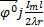sinθ ; (2.12)

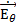(r, θ, t) = 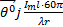sinθ . (2.13)

Особенности (свойства) ЭМП в дальней (волновой) зоне:

1) Электрическое 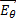и магнитное 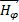носят волновой характер (об этом свидетельствует волновой множитель) .

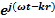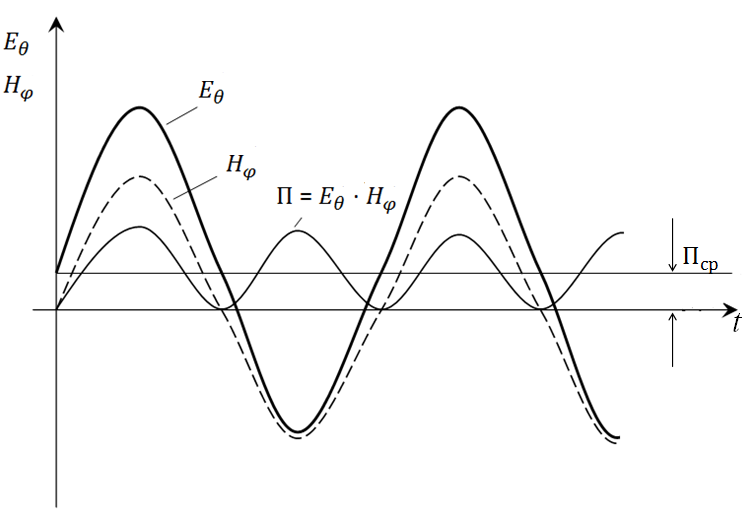
Рисунок 2.10 – Поле ЭЭВ в дальней зоне

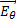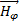2) Поля и синфазны, следовательно, энергия в волновой зоне активна, т.е. уходит от вибратора и назад не возвращается.

3) Векторы 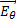и 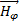взаимно перпендикулярны в пространстве ().
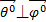Определим направление вектора Пойнтинга.

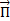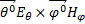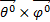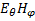= = () = П. (2.14)

То есть вектор Пойнтинга направлен по радиусу. Это значит, что электромагнитная энергия распространяется по радиусам по всем направлениям.

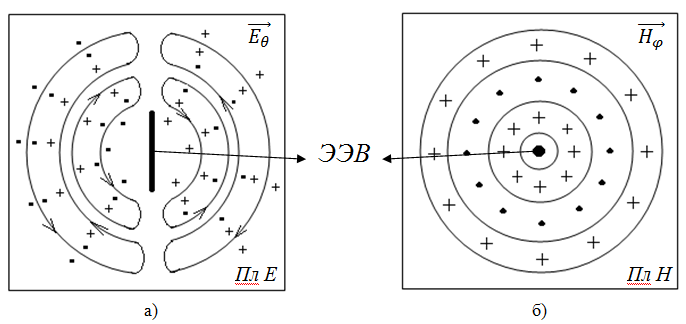
Рисунок 2.11 – Структура поля ЭЭВ в дальней зоне

Силовые линии электрического поля лежат в меридиальных плоскостях (рис. 2.11, а). Силовые линии магнитного поля лежат в плоскостях, перпендикулярных оси вибратора (рис. 2.11, б).

4) Фронт волны сферический. Действительно, во фронте волны фаза
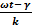γ ωt-kr = const. Откуда r = ипри t = const, r = const. Это уравнение сферы.

5) Амплитуды полей убывают с удалением от вибратора пропорционально 1/r. Это объясняется расширением сферического фронта волны, т.е. рассеиванием электромагнитных волн в пространстве (рис. 2.12).

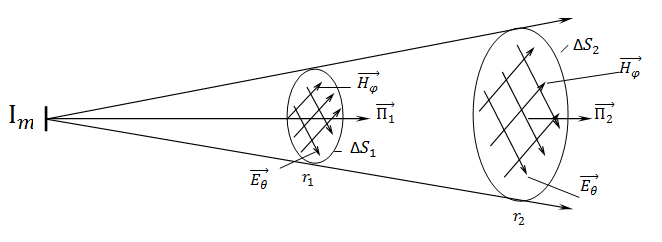
Рисунок 2.12 –Рассеивание электромагнитных волн в пространстве

На расстоянии от вибратора плотность мощности = 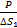, на расстоянии 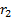– 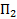= 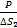. То есть 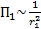, а 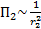. Модуль вектора Пойнтинга пропорцианален квадрату напряженности электрического (магнитного) поля

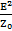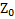П = ЕН = Е = = H H = 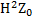. (2.15)

Тогда напряженности электрического и магнитного полей убывают пропорционально 1/r. Мгновенное распределение поля в пространстве изображено на рисунке 2.13.

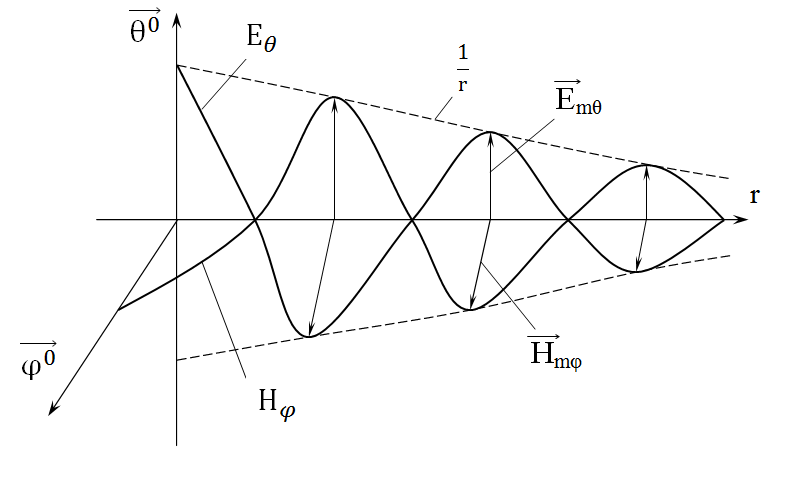
Рисунок 2.13 – Мгновенное распределение поля в пространстве

дальной зоны

6) Амплитуда ЭМП обратно пропорциональна длине волны, т.е. пропорциональна частоте. Следовательно, для увеличения интенсивности излучения следует увеличивать частоту колебаний.

7) Амплитуды 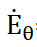и 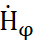зависят от θ по закону sinθ, а от φ не зависят.