Это прямолинейный излучатель (рис. 2.1), удовлетворяющий условиям: l<< λ, d<<l и I (l) = const, т.е. в данный момент времени ток вдоль всего излучателя имеет одно и то же значение. Ток, текущий по вибратору, создает вокруг него кольцевое магнитное поле  . Возникающие на концах вибратора заряды создают электрическое поле, лежащее в плоскости вибратора.
. Возникающие на концах вибратора заряды создают электрическое поле, лежащее в плоскости вибратора.
Элементарный электрический вибратор применяется для расчета проволочных (вибраторных) антенн.

Рисунок 2.1 – Элементарный электрический вибратор
Элементарный магнитный вибратор
Это плоский виток с током, равномерно распределенным по контуру. Условие элементарности вибратора  <<λ, где S – площадь ограниченная витком (рис. 2.2).
<<λ, где S – площадь ограниченная витком (рис. 2.2).
Этот вибратор применяют к расчету щелевых и рамочных антенн.

Рисунок 2.2 – Элементарный
магнитный вибратор
Элемент Гюйгенса
Это бесконечно малый участок фронта волны (рис. 2.3). Условие элементарности l<<λ. При этом в пределах элемента амплитуда электрического и магнитного поля постоянны. Элемент Гюйгенса применяют для расчета рупорных, зеркальных, линзовых антенн и фазированных антенных решеток.

Рисунок 2.3 – Элемент Гюйгенса
Электромагнитное поле излучения электрического
Вибратора
Поместим элементарный электрический вибратор (ЭЭВ) в начале сферической системы координат (рис. 2.4, а). Орты системы 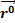 ,
, 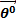 ,
, 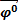 образуют правую тройку векторов
образуют правую тройку векторов 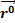 =
= 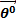 ×
× 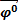 . Полагаем, что нам надо определить ЭМП, т.е. векторы
. Полагаем, что нам надо определить ЭМП, т.е. векторы  и
и 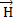 в точке М, имеющую координаты r, θ, φ (рис. 2.4,б).
в точке М, имеющую координаты r, θ, φ (рис. 2.4,б).
| а | б |

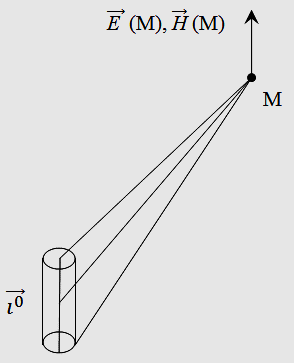
Рисунок 2.4 – Сферическая система координат, в её центре – ЭЭВ
Пусть по вибратору течет высокочастотный ток с постоянной амплитудой  (l) = const.
(l) = const.
Поясним процесс излучения электромагнитной энергии в пространство.
Для наглядности рассмотрим симметричный, т.е. имеющий два плеча электрический вибратор (l = λ / 2), полученный из двухпроводной линии, контуры которой разведены на 180° (рис. 2.5,а). Для простоты будем рассматривать изменение напряженности электрической составляющей ЭМП в пространстве. Магнитная составляющая будет вести себя аналогично.
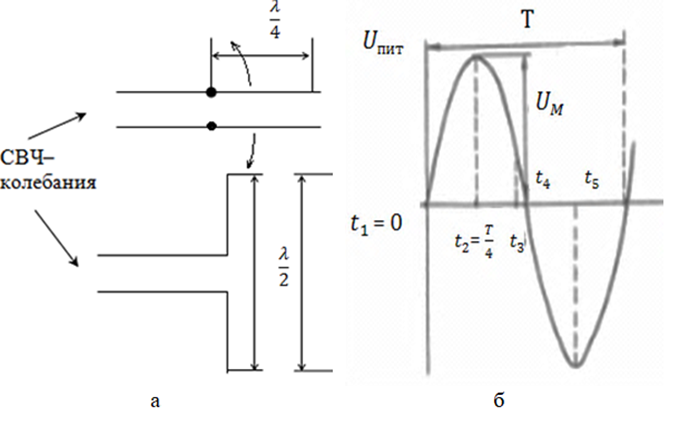 Рисунок 2.5 – К процессу излучения электромагнитных волн Рисунок 2.5 – К процессу излучения электромагнитных волн |
Выберем за начальный момент 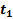 = 0, момент, когда питающее антенну напряжение (ток) высокочастотных колебаний с периодом Т равно 0. В пространстве вокруг антенны напряженность электрического поля в этот момент также равна нулю.
= 0, момент, когда питающее антенну напряжение (ток) высокочастотных колебаний с периодом Т равно 0. В пространстве вокруг антенны напряженность электрического поля в этот момент также равна нулю.
Через четверть периода 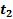 =
=  подведенные к антенне СВЧ-колебания достигнут своего максимума и в пространстве вокруг антенны возникает электрическое поле, направление силовых линий которого показано на рисунке 2.6,б. Причем за время от
подведенные к антенне СВЧ-колебания достигнут своего максимума и в пространстве вокруг антенны возникает электрическое поле, направление силовых линий которого показано на рисунке 2.6,б. Причем за время от 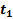 = 0 до
= 0 до 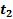 электромагнитное поле удалится от антенны на расстояние λ/4. Затем напряжение, подводимое к антенне, начнет уменьшаться, и концы силовых линий электрического поля будут как бы стягиваться к середине антенны (рис. 2.6, в). В момент времени
электромагнитное поле удалится от антенны на расстояние λ/4. Затем напряжение, подводимое к антенне, начнет уменьшаться, и концы силовых линий электрического поля будут как бы стягиваться к середине антенны (рис. 2.6, в). В момент времени  =
=  ,
,  = 0,
= 0,
а концы силовых линий электрического поля соединяются, образуя замкнутые петли (рис. 2.6,г). Электромагнитное поле к этому времени удалится от антенны на расстояние, равное λ/2. В 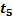 =
=  Т напряжение по абсолютной величине вновь станет максимальным, а направление силовых линий вектора
Т напряжение по абсолютной величине вновь станет максимальным, а направление силовых линий вектора  будет противоположным направлению
будет противоположным направлению  в момент времени
в момент времени 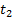 . Электрическое поле, возникшее вокруг антенны в момент времени
. Электрическое поле, возникшее вокруг антенны в момент времени 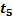 в непосредственной близости от нее, как бы «отжимает» то поле, которое уже потеряло связь с антенной. Рассмотренный процесс повторяется периодически, т.е. – это колебательный электромагнитный процесс, охватывающий все новые и новые области пространства.
в непосредственной близости от нее, как бы «отжимает» то поле, которое уже потеряло связь с антенной. Рассмотренный процесс повторяется периодически, т.е. – это колебательный электромагнитный процесс, охватывающий все новые и новые области пространства.
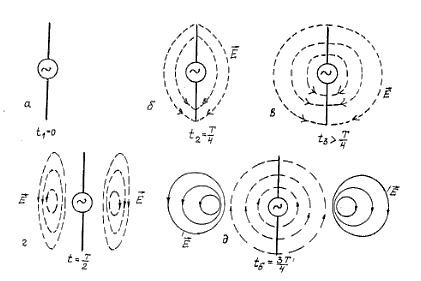
Рисунок 2.6 – Пояснение излучения радиоволн симметричным вибратором
Сформулируем необходимые условия эффективного излучения электромагнитных волн антенной.
Первое условие состоит в том, что заряды (напряжение) в антенне должны исчезать и накапливаться быстро, иначе говоря, переменный ток, протекающий в антенне, должен иметь значительную частоту. Чем выше частота тока в антенне, тем эффективней она излучает, поэтому для передачи сигналов (информации) с помощью электромагнитных волн используют высокочастотные колебания.
Второе условие состоит в том, что поле антенны должно охватывать возможно больший объём, иначе говоря, размеры антенны L должны быть сравнимы с длиной излучаемой волны L ~ λ.
Приведем выражения для составляющих ЭМП, излучаемого элементарным электрическим вибратором без доказательств
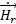 = 0;
= 0;  = 0;
= 0;
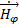 (r, θ) =
(r, θ) = 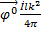 (
( +
+ 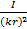 ) sinθ
) sinθ 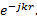 (2.1)
(2.1)
По найденному значению напряженности магнитного поля, используя выражение 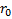 t
t 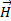 = jω
= jω  , найдем выражения для компонент электрического поля
, найдем выражения для компонент электрического поля
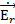 (r, θ) =
(r, θ) = 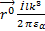 (
(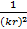 –
– 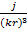 ) cosθ
) cosθ 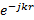 ;(2.2)
;(2.2)
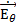 (r, θ) =
(r, θ) = 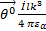 (
(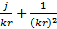 –
– 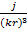 ) sinθ
) sinθ 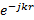 ; (2.3)
; (2.3)
 (r, θ) = 0.
(r, θ) = 0.
Проведем анализ поля элементарного вибратора, описываемого выражениями (2.1), (2.2), (2.3).
Из формулы (2.1) следует, что магнитное поле имеет только азимутальную составляющую. В этом проявляется сходство с магнитным полем постоянного электрического тока, протекающего по линейному проводнику (силовые линии  – концентрические окружности, охватывающие ток).
– концентрические окружности, охватывающие ток).
Из формул (2.2) и (2.3) следует, что вектор напряженности электрического поля имеет составляющие, ориентированные по ортам 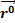 и
и 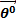 , т.е. лежит в плоскости вибратора.
, т.е. лежит в плоскости вибратора.
Из формул (2.1) – (2.3) видно, что компоненты векторов  и
и  зависят от координат θи r, а от φ не зависят. Это естественно, т.к. вибратор – осесимметричный излучатель, поэтому все направления по азимуту (φ) для него равноценны.
зависят от координат θи r, а от φ не зависят. Это естественно, т.к. вибратор – осесимметричный излучатель, поэтому все направления по азимуту (φ) для него равноценны.
Каждое из соотношений (2.1) – (2.3) может быть представлено в виде:
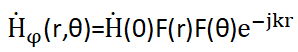 (2.4)
(2.4)
| где | 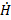 (0) (0) | – | значение поля в начале координат; |
| F(r) | – | закон изменения амплитуды поля с удалением от вибратора (по координате r); | |
| F(θ) | – | закон изменения интенсивности поля по направлению (по координате θ); | |
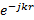 | – | множитель запаздывания, показывающий, что рассматриваемое поле представляет собой сферическую волну |
Действительно, пусть ток вибратора изменяется по гармоническому закону, т.е. 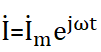 , тогда в рассмотренных выражениях получим волновой множитель
, тогда в рассмотренных выражениях получим волновой множитель  , т.е.
, т.е.  и
и 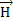 – это электромагнитное поле, «бегущее» в направлении увеличения радиуса r. В этом легко убедиться следующим образом. На фронте волны фаза постоянна γ = ωt – kr. Определим геометрическое место точек с одинаковыми фазами
– это электромагнитное поле, «бегущее» в направлении увеличения радиуса r. В этом легко убедиться следующим образом. На фронте волны фаза постоянна γ = ωt – kr. Определим геометрическое место точек с одинаковыми фазами
r = 
При t=const получим r=const. А это и есть уравнение сферы с радиусом r.
Таким образом, элементарный электрический вибратор, как и любой элементарный (точечный) излучатель, излучает сферические волны.
Теперь определим характер функции F(r). Построим графики зависимости
F(r) = 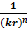 (рис. 2.7).
(рис. 2.7).
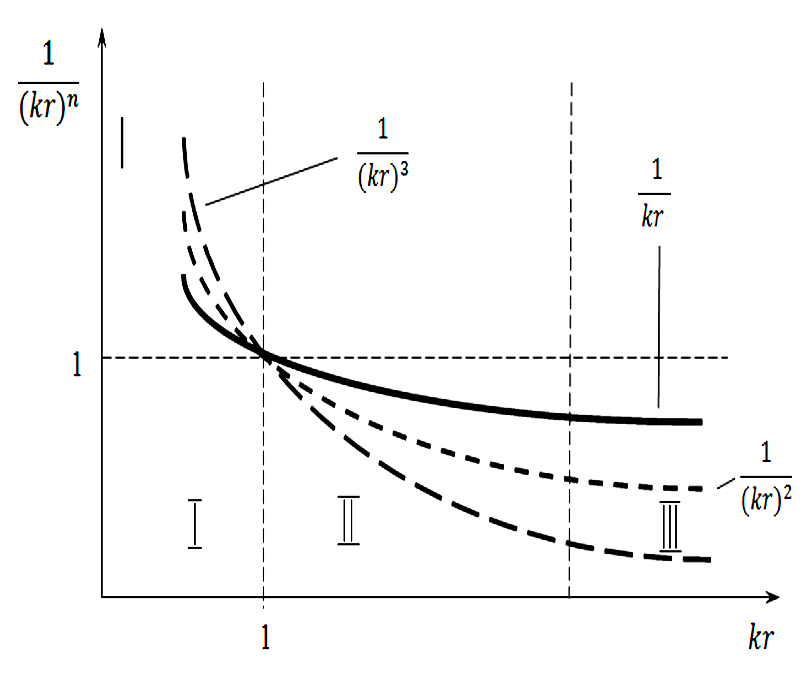
Рисунок 2.7 – Изменение интенсивности составляющих ЭМП (F(r) =  ) в зависимости от удаления до вибратора, где n = 1, 2, 3
) в зависимости от удаления до вибратора, где n = 1, 2, 3
В зависимости от расстояния до вибратора r различают три зоны:
I – ближняя или реактивная зона, в которой kr<< 1;
II – промежуточная зона или зона Френеля kr≈1;
III – дальняя зона или зона Фраунгофера, в которой kr>> 1.
 2017-12-14
2017-12-14 6950
6950








