1.
Сложение. Так как комплексное число можно интерпретировать как точку на комплексной плоскости, то если
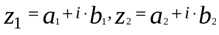 , имеем:
, имеем: 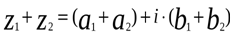
Например:
(3+2i) + (-4+7i) = (3-4)+(2+7)I = -1+9i.
2.
Умножение.
а). Если числа заданы в алгебраической форме, имеем:
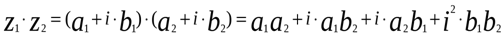 .
.
Учитывая, что 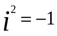 , имеем:
, имеем:
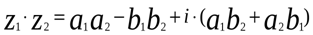 .
.
в). Если числа заданы в комплексной форме 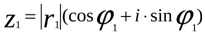 и
и 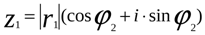 , то
, то 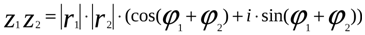 .
.
При доказательстве мы используем формулы синуса суммы и косинуса суммы двух углов (проделайте самостоятельно).
3.
Деление.
а). Если числа заданы в алгебраической форме, то числитель и знаменатель домножим на сопряженное к знаменателю число, чтобы в знаменателе получилось действительное число. Имеем:
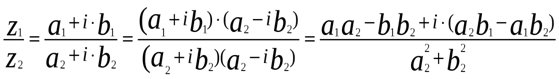
(проделайте вычисления самостоятельно, учитывая равенство 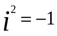 ).
).
в). Если числа заданы в комплексной форме 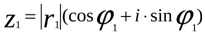 и
и 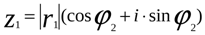 , то
, то
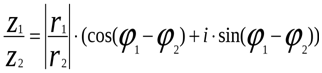 , если
, если 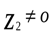 .
.
Формулу произведения двух комплексных чисел можно обобщить на n сомножителей. Отсюда, как частный случай, получается формула:
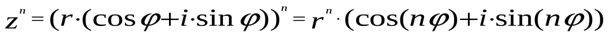
^ 5. Извлечение корня n-ой степени.
Имеет место формула Муавра:
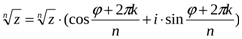 , где
, где 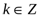 .
.
Таким образом, комплексное число z имеет бесконечно много корней n-ой степени, причем различных корней – ровно n штук. Все корни расположены на окружности радиуса 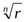 в вершинах правильного n-угольника.
в вершинах правильного n-угольника.
Пример 3.
Вычислить 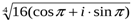 .
.
Решение: По формуле Муавра имеем:
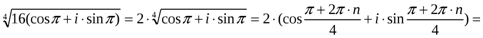
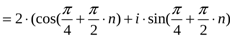 ,
, 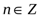
При различных значениях n получим все корни комплексного числа. Среди них имеются ровно четыре различных. Их можно получить, подставляя значения n:
При  имеем:
имеем: 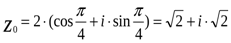 .
.
При  имеем:
имеем: 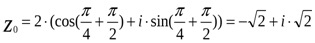 .
.
При 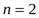 имеем:
имеем: 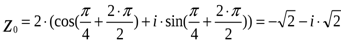 .
.
При  имеем:
имеем:  .
.
Все эти корни находятся на окружности радиуса  в вершинах правильного четырехугольника (квадрата) (см. рис. 3)
в вершинах правильного четырехугольника (квадрата) (см. рис. 3)
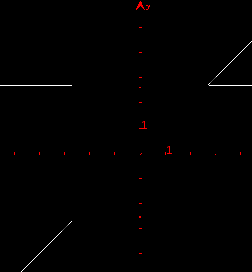
Рис. 3.
Пример 4. Вычислить 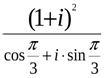 . Ответ записать в алгебраической форме.
. Ответ записать в алгебраической форме.
Решение. Вычислим выражение, стоящее в числителе, результат запишем в тригонометрической форме
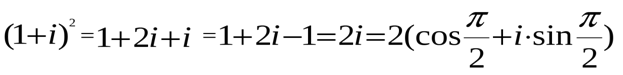
Подставим полученное число в числитель и применим формулу деления комплексных чисел, записанных в тригонометрической форме:
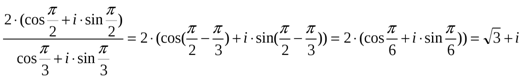 .
.
Ответ: 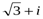 .
.
Решение уравнений.
1.
Решение рациональных уравнений n-ой степени.
Из основной теоремы алгебры известно, что каждое алгебраическое уравнение степени n имеет во множестве комплексных чисел ровно n корней.
Рассмотрим уравнение
 ,
,
где коэффициенты 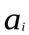 (i = 0,1, 2,…,n) – действительные числа. Основной метод решения таких уравнений – разложение на множители. При этом, среди множителей могут быть линейные вида
(i = 0,1, 2,…,n) – действительные числа. Основной метод решения таких уравнений – разложение на множители. При этом, среди множителей могут быть линейные вида  и тогда
и тогда 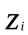 является корнем уравнения и квадратичные
является корнем уравнения и квадратичные 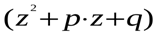 . Решая квадратное уравнение
. Решая квадратное уравнение 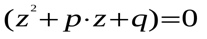 , можем получить:
, можем получить:
1.
два различных действительных корня, если 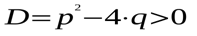
2.
два совпадающих действительных корня, если 
3.
два комплексных (сопряженных) корня, если  .
.
Пример 5. Решить уравнение:
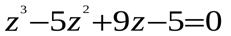
Решение. Преобразуем левую часть уравнения для того, чтобы применить метод группировки:
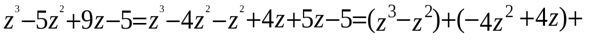
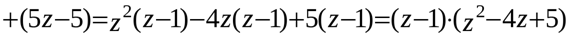
Тогда уравнение примет вид:

 или
или 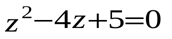
 или
или 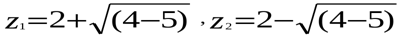 .
.
Учитывая, что 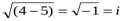 , получим
, получим 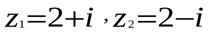 .
.
Ответ: корни уравнения 
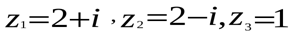 .
.
2.
Решение уравнений произвольного вида.
Другой способ решения уравнений основывается на том, что если 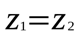 , то
, то
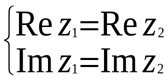
Таким образом, необходимо отделить действительные и мнимые части уравнения, приравнять их и решить полученную систему уравнений.
Пример 6. Решить уравнение 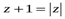 .
.
Решение. Пусть 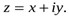 Тогда уравнение имеет вид:
Тогда уравнение имеет вид: 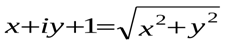 . Отделив действительные и мнимые части в обеих частях равенства, получим:
. Отделив действительные и мнимые части в обеих частях равенства, получим:
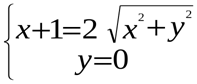

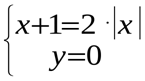
Решим уравнение 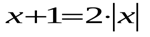 Оно эквивалентно совокупности двух систем:
Оно эквивалентно совокупности двух систем:
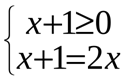 или
или 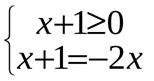
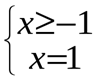
 или
или 
Оба корня 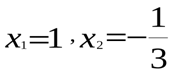 удовлетворяют условию
удовлетворяют условию  . Возвращаясь к системе, получим:
. Возвращаясь к системе, получим: 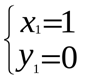 или
или  . Вспоминая, что
. Вспоминая, что 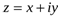 , получим ответ.
, получим ответ.
Ответ: 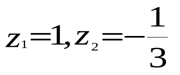 .
.
 2017-12-14
2017-12-14 1696
1696
