В заключение исследуем геометрический смысл уравнений и неравенств с комплексными числами. Так как каждое комплексное число представляет собой точку на комплексной плоскости, то уравнение с комплексными числами задает на плоскости линию. Укажем некоторые из них.
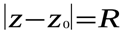 . (а)
. (а)
Так как 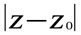 есть расстояние между точками
есть расстояние между точками 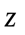 и
и 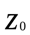 , то данная линия определяется как множество точек
, то данная линия определяется как множество точек 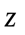 , расстояние от каждой из которых равно
, расстояние от каждой из которых равно 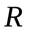 . Это – уравнение окружности с центром в точке
. Это – уравнение окружности с центром в точке 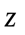 и радиуса
и радиуса 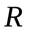 .
.
То же самое можно получить, положив 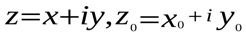 и подставив эти точки в уравнение. Т. к.
и подставив эти точки в уравнение. Т. к. 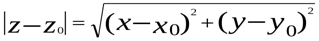 , то
, то 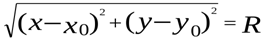 , или
, или 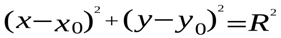 - уравнение окружности.
- уравнение окружности.
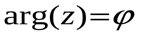 . (б)
. (б)
Это – уравнение луча, выходящего из точки (0,0) под углом 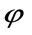 к положительному направлению оси Ox. При этом, так как для точки
к положительному направлению оси Ox. При этом, так как для точки 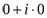 аргумент не определен, то точка (0,0) является «выколотой».
аргумент не определен, то точка (0,0) является «выколотой».
Пример 7. Изобразить на комплексной плоскости линию, задаваемую уравнением 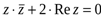 .
.
Решение: Пусть 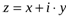 . Тогда
. Тогда 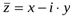 и уравнение примет вид:
и уравнение примет вид:
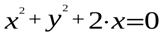 . Выделим полный квадрат:
. Выделим полный квадрат: 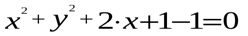 . Получим:
. Получим: 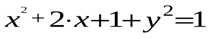 , или
, или 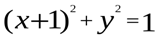 - уравнение окружности с центром в точке (-1,0) и радиуса 1.
- уравнение окружности с центром в точке (-1,0) и радиуса 1.
Неравенство с комплексными числами задает на плоскости область, ограниченную соответствующей линией.
а). 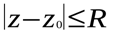 задает на плоскости внутренность окружности (см рис 4 а).)
задает на плоскости внутренность окружности (см рис 4 а).)
б). 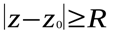 задает на плоскости внешнюю часть окружности (см рис 4 б).)
задает на плоскости внешнюю часть окружности (см рис 4 б).)
в). 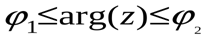 задает на плоскости внутренность угла, ограниченного лучами
задает на плоскости внутренность угла, ограниченного лучами
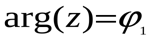 и
и 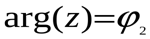 . (см. рис. 4 в).)
. (см. рис. 4 в).)
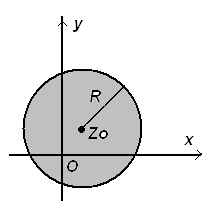
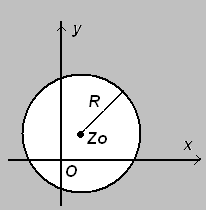
Рис. 4а) Рис. 4б)
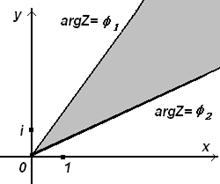
Рис. 4в)
Пример 8. Изобразить на плоскости множество точек, задаваемых системой неравенств 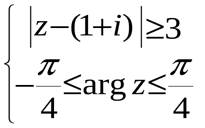 .
.
Первое неравенство задает на плоскости внешнюю область окружности с центром в точке (1,1) и радиуса 3, вторая область задает внутренность угла со сторонами 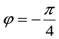 и
и 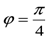 . Общая область – пересечение этих двух областей (см. рис 5.).
. Общая область – пересечение этих двух областей (см. рис 5.).
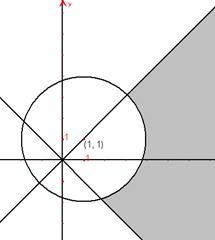
Рис. 5
Представленные ниже задачи являются контрольным заданием для учащихся 10 классов. Решения необходимо оформить в отдельной тетради и выслать по адресу 680000, г. Хабаровск, ул. Дзержинского, 48, ХКЦТТ, ХКЗФМШ. Для зачета нужно набрать не менее 30 баллов. В решениях следует делать необходимые пояснения и рисунки, дающие представления о ходе Ваших рассуждений.
М.10.1.1. Записать комплексные числа в алгебраической и тригонометрической форме, отметить их на комплексной плоскости (5 баллов за пример).
а). 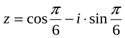 , б).
, б). 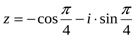 , в).
, в). 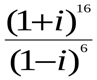
М.10.1.2. Выполнить действия. Ответ записать в алгебраической форм (5 баллов за пример).
а). 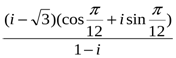 б).
б). 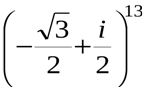 в).
в). 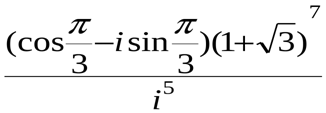
М.10.1.3. Вычислить все различные корни их комплексного числа и нанести их на комплексную плоскость (5 баллов за пример).
а). 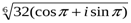 б).
б). 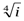 в).
в). 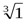 г).
г). 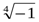
М.10.1.4. Решить уравнения (10 баллов за пример).
а). 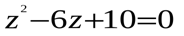 б).
б). 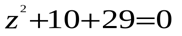 в).
в). 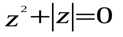 г).
г). 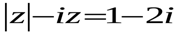
М.10.1.5. При каких значениях параметра a уравнение имеет комплексные корни? (10 баллов за пример).
а). 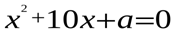 б).
б). 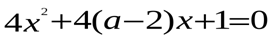
Найти эти корни при каком-либо значении параметра.
М.10.1.6. Какое множество точек на комплексной плоскости задается условием?? (10 баллов за пример).
а). 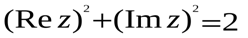 б).
б). 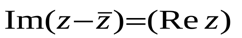 в).
в). 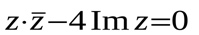
г). 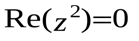 д).
д). 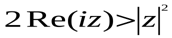 е).
е). 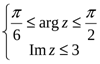
Изобразить найденное множество на комплексной плоскости.
 2017-12-14
2017-12-14 8756
8756