Проекции топографических карт

Топографические карты масштабов: 1:25000, 1:50000, 1:100000, 1:200000, 1:500000 составляются в

единой равноугольной поперечно–цилиндрической проекции Гаусса

(немецкий математик 1777–1855г.). Геометрическая сущность проекции, в которой изготовляются топографические карты заключается в следующем. Вся поверхность земного эллипсоида разбивается по меридианам на 60 зон по 6° каждая, и карты составляются для каждой зоны в отдельности. Средний меридиан в каждой зоне называется осевым меридианом, он делит зону на две равные части – западную и восточную. Счет зон ведется с запада на восток от начального меридиана, за который принят Гринвичский меридиан, проходящий через Гринвичскую обсерваторию (в окрестностях Лондона).

Чтобы представить себе, как получается на плоскости изображение этих зон, вообразим цилиндр, который по осевому меридиану одной из зон касается глобуса, изображающего в данном масштабе земной шар. Зону спроектируем на боковую поверхность цилиндра, так чтобы при этом сохранилось свойство равноугольности изображения, т.е. равенство всех углов их действительной величине на глобусе. Таким же способом последовательно спроектируем на боковую поверхность цилиндра все остальные зоны, одну рядом с другой. Разрезав теперь цилиндр по образующей АА₁ или ВВ₁, и развернув его боковую поверхность в плоскость, получим изображение земной поверхности в виде отдельных зон, соприкасающихся одна с другой лишь в точках касания по экватору. Изображение каждой зоны, полученное таким образом в нужном масштабе, делится сеткой меридианов и параллелей на отдельные листы карты установленного размера. Рассмотрим основные геометрические свойства полученного изображения зоны. Осевой меридиан в каждой зоне и экватор изображается прямыми линиями, причем осевые линии 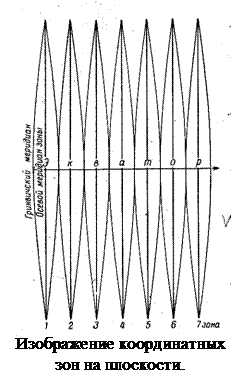Так как, при проектировании цилиндр соприкасается с каждой зоной по осевому меридиану, очевидно, что все эти меридианы изображаются в данной проекции без искажения длин и сохраняют масштаб на всём своём протяжении. Остальные меридианы в каждой зоне изображаются в проекции кривыми линиями, поэтому все они длиннее осевого меридиана, т.е. искажены. Все параллели тоже изображаются кривыми и с некоторым искажением.

Эти искажения длин всех линий увеличиваются по мере удаления от осевого меридиана на восток и запад. Наибольшие искажения получаются на краях зоны, где они могут достигать величины порядка 1/1000 длины линии, измеряемой по карте. Это значит, что если, например, вдоль осевого меридиана, где нет искажений длин, масштаб карты равен 500 м в 1 см, то на краю зоны он будет равен 499,5 м в 1 см.

Таким образом, теоретически нашим топографическим картам также присущи искажения длин и переменный масштаб. Однако эти искажения при измерениях на картах практически не ощутимы, поэтому масштаб любой топографической карты для всех её участков можно считать постоянным.