Проверка статистических гипотез. Статистической гипотезой называется предположение относительно вида и параметров распределения случайной величины

Общие сведения.

Статистической гипотезой называется предположение относительно вида и параметров распределения случайной величины, которое можно проверить статистически, используя результаты наблюдений. При проверке гипотез подвергается испытанию некоторая основная (нулевая) гипотеза Н ₀ в сравнении с одной или несколькими альтернативными (конкурирующими) гипотезами Н ₁, Н ₂, …, которые формируются или подразумеваются.

Под статистическим критерием (критерием проверки или значимости) понимают однозначно определенное правило, согласно которому устанавливаются условия принятия или непринятия гипотезы. При проверке статистической гипотезы всегда есть риск совершить одну из двух ошибок: отвергнуть верную гипотезу (ошибка первого рода) или принять ложную гипотезу (ошибка второго рода).

Вероятность ошибки первого рода зависит от принятого уровня значимости a, под которым понимают вероятность появления практически невозможных событий, т.е. таких событий, вероятность появления которых весьма мала. Обычно при решении задач надежности технологического оборудования принимают a = 0,05.

Вероятность ошибки второго рода зависит от уровня, характера проверяемой гипотезы, от способа проверки и ряда других причин, что затрудняет её оценку. Снижение уровня значимости приводит к увеличению вероятности ошибки второго рода, и поэтому единственным способом одновременного уменьшения ошибок обоих типов является увеличение объёма выборки.

Рассмотрим основные типы задач, решаемые с помощью статистических критериев.

Сравнение дисперсий.

Пусть имеются две независимые выборки n ₁ и n ₂, по которым определены статистические характеристики , , и . Требуется проверить можно ли считать сравниваемые выборочные дисперсии оценками одной и той же генеральной дисперсии.

Допустим, что первая выборка сделана из генеральной совокупности с дисперсией , а вторая - из генеральной совокупности с дисперсией . Нулевая гипотеза Н ₀ состоит в том что . Для того, чтобы её отвергнуть, необходимо доказать значимость различий между 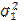и при выбранном уровне значимости a. Пусть , тогда альтернативной гипотезой Н ₁ будет . Нулевую гипотезу обычно проверяют по критерию Фишера, для чего вычисляют величину и сравнивают её с критическим значением F _a, которое находится по таблице (Приложение Ж). F _a зависит от уровня значимости a и степеней свободы больше f ₁ = n ₁–1 и меньшей f ₂ = n ₂–1 дисперсий. Если , то различие между дисперсиями следует считать значимым, и нулевая гипотеза Н ₀ () отвергается. При гипотеза принимается.

Пример 1.10. При изучении стабильности работы двух датчиков температуры получены две выборки объёмом n ₁ = 8 и n ₂= 11 с выборочными дисперсиями и . Проверить гипотезу Н ₀: .

Решение.

Вычислим величину

По таблице (Приложение Ж) для уровня значимости a = 0,05 и числа степеней свободы f ₁ = 7 и f ₂ = 10 находим F _0,05 = 3,14. Поскольку , то гипотеза Н ₀ принимается, и поэтому разница дисперсий для обоих датчиков незначима. Это позволяет считать случайные погрешности обоих датчиков одинаковыми.

Для сравнения нескольких дисперсий , имеющих числа степеней свободы , используют критерий Бартлета, а при одинаковом объёме всех выборок критерий Кохрена.

Сравнение средних.

При рассмотрении вопросов надежности часто возникает необходимость сравнить два технологических процесса, агрегат или метода измерения. В этом случае обычно сравнивают средние значения.

Пусть заданы две выборки x ₁, x ₁, …, x _n₁ и y ₁, y _{1, …,} y _n₂. Выдвигается нулевая гипотеза Н ₀ о совпадении средних значений двух генеральных совокупностей, т.е. . При этом различают зависимые и независимые выборки.

Случай зависимых или связанных выборок имеет место, например, при измерении одних и тех же параметров двумя различными способами: механическим и электрическим, механическим и оптическим и т.д. Принимая объёмы выборок одинаковыми, т.е. n = n ₁ = n ₂, и вычисляя значения разностей для каждой пары измерений d_i = x_i – y_i, получим выборку новой случайной величины d_i объёмом n и статистическими параметрами

, .

Считая, что ряд значений d_i представляет собой выборку из нормально распределенной генеральной совокупности со средним значением M[d] = 0 и неизвестной дисперсией , вычисляется величина t, имеющая распределение Стьюдента с числом степеней свободы f = n -1:

Гипотеза Н ₀ принимается, если величина t будет меньше табличного значения t_a. При t > t_a гипотеза отвергается, и средние значения двух выборок считаются различными с вероятностью b = 1- a.

В случае независимых выборок объемы выборок могут быть различными и для проверки нулевой гипотезы Н ₀ вычисляется величина t, имеющая распределение Стьюдента с числом степеней свободы f = n ₁+ n ₂ - 2:

Если табличное значение t_a для заданного уровня значимости a и числа степеней свободы f будет больше вычисленного значения t, то гипотеза принимается. При t > t_a гипотеза о равенстве средних двух выборок отвергается. Если объём выборок одинаков, т.е. n = n ₁ = n ₂, то приведенная формула упрощается.

Пример 1.11. Сравнивается работа двух прессов. Среднемесячная выработка (n =25) на одном прессе составила т с дисперсией , на втором - т с дисперсией .