Интервальные оценки параметров нормального распределения

Для того чтобы дать представление о точности и достоверности оценки искомых параметров в математической статистике используют понятия доверительного интервала и доверительной вероятности.

Пусть по результатам n опытов для математического ожидания M[X] получена оценка . Зададим достаточно большую вероятность β с тем, чтобы событие с вероятностью β можно было считать практически достоверным. При решении задач надежности металлургического оборудования обычно принимают β = 0,90 или β = 0,95.

Вероятность того, что отклонение D х математического ожидания M[X] от среднего арифметического значения не превосходит по абсолютной величине некоторого заданного значения e, можно задать в следующем виде

Это выражение означает, что с вероятностью β неизвестное значение M[X] попадет в интервал J_β от ( - e) до ( + e).

Интервал J_β называется доверительным интервалом. Вероятность β называется доверительной вероятностью. Границы доверительного интервала x’ = ( - e) и x” = ( + e) – доверительными границами.

Ошибки, возникающие при замене M[X] на и превышающие малую величину e, будут появляться с малой вероятностью a = 1 – β, которая называется уровнем значимости.

Ширина доверительного интервала характеризует точность, а доверительная вероятность – достоверность оценки математического ожидания M[X] с помощью выборочного среднего . Очевидно, что чем больше требуется достоверность, тем больше при том же объеме выборки должен быть доверительный интервал.

Для нахождения доверительного интервала надо знать закон распределения величины D х. Поскольку величина зависит от суммы n независимых случайных величин x_i, то при достаточно большом n (на практике при n > 10…20) её закон распределения близок к нормальному со средним значением M[X] и средним квадратичным отклонением .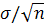

Если величина дисперсии известна, то

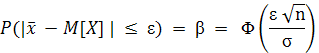
где Φ – функция Лапласа. Задавшись доверительной вероятностью β (или уровнем значимости a = 1 – β) по таблице 1.1 для значения функции Φ(u) = β/2 определяется аргумент функции Лапласа 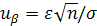и затем доверительный интервал для математического ожидания

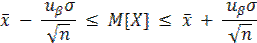
Если величина дисперсии неизвестна, что часто имеет место на практике, то доверительный интервал определяют по формуле

Здесь t_a - коэффициент Стьюдента, значения которого даны в таблице 1.3 в зависимости от уровня значимости a = 1 – β и числа степеней свободы f; s – оценка среднеквадратичного отклонения σ. Если выборочная дисперсия s² и среднее арифметическое значение определяются по одной и той же выборке, то f = n – 1.

Таблица 1.3 – Значения Критерия Стьюдента t_a в зависимости от числа степеней свободы f для уровня значимости и a = 1 – β = 0,05.

f	t_a	f	t_a	f	t_a
	12,71		2,37		2,12
	4,30		2,31		2,10
	3,18		2,26		1,09
	2,78		2,23		2,06
	2,57		2,18		2,04
	2,45		2,15	∞	1,96

Аналогично определяется доверительный интервал для дисперсии. При достаточно большом числе степеней свободы (f > 30) доверительные границы для среднеквадратичного отклонения определяются неравенством

Пример 1.9. Предполагая в примере 1.7, что величина ежесуточного выпуска поковок распределена по нормальному закону, найти для среднеарифметического значения = 15,4 т/сут и дисперсии s ² = 53,2 (т/сут)² доверительные интервалы при доверительной вероятности β = 0,95 (уровень значимости a = 1 – β = 0,05).

Решение.

По таблице 1.3 для f = n – 1 = 35 и a = 1 – β = 0,05 находим путем линейной интерполяции t_0,05 = 2,02. Поэтому

Следовательно, с доверительной вероятностью 0,95 можно считать, что математическое ожидание ежесуточного выпуска поковок лежит в интервале от ( - e) = 15,4 - 2,5 = 12,9 т/сут до ( + e) = 15,4 + 2,5 = 17,9 т/сут.

По таблице 1.2 для значения функции Лапласа Φ(u) = β/2 = 0,475 путем линейной интерполяции находим значение u _0,05 = 1,91. Следовательно, с доверительной вероятностью 0,95 можно считать, что среднеквадратичное отклонение лежит в диапазоне