Определение параметров закона распределения

 

Разработка методов регистрации, описания и анализ статистических данных, полученных в результате наблюдения массовых случайных явлений, составляет предмет математической статистики. В отличие от теории вероятностей, которая оперирует с характеристиками теоретического распределения случайных величин, математическая статистика занимается правилами получения, обработки и истолкования эмпирического распределения.

Основной задачей математической статистики является определение по известному эмпирическому распределению частот соответствующего ему теоретического распределения вероятностей. В общем случае задача достаточно сложна, но она значительно упрощается, если вид функции распределения можно предсказать заранее. Так, если исследуемое распределение случайной величины является нормальным, то задача состоит в оценке математического ожидания и дисперсии, которые полностью определяют это распределение.

Допустим, что в результате n измерений случайной величины Х получена последовательность значений х ₁, х ₂, …, х _n,, которая называется простым статистическим рядом или выборкой из генеральной совокупности. Под генеральной совокупностью понимают все допустимые значения случайной величины. Выборка называется презентативной (представительной), если она дает достаточно хорошее представление об особенностях генеральной совокупности. Обычно выборка оформляется в виде таблицы, в первой колонке которой стоит номер опыта i, а во второй – значение случайной величины.

Первичная обработка выборки состоит в группировке найденных значений по достаточно малым интервалам, вычислении средних относительных частот для каждого интервала и графическом представлении результатов в виде гистограммы или эмпирической функции распределения.

Число интервалов, на которое следует группировать выборку, должно быть не слишком мало, так как при малом числе интервалов распределение случайной величины описывается слишком грубо, а, с другой стороны, не слишком велико, поскольку в этом случае теряется закономерность колебаний эмпирических частот. Число интервалов k можно определить по формуле

Полученное значение округляют до ближайшего целого числа. Практика показывает, что число интервалов не должно превышать 10-20.

Ширина интервалов D х, как правило, выбирается одинаковой и равной

Все значения случайной величины, попавшие в некоторый интервал, относятся к его середине.

Пример 1.1. Ежесуточный выпуск кузнечным цехом поковок m (т/сут) регистрировался в течение n = 36 суток. Результаты даны в таблице.

I
M	1,8	32,7	3,6	1,9	25,1	25,4	5,3	6,6	24,7
I
M	6,9	7,7	25,2	8,8	23,0	9,7	11,3	20,7	21,2
I
M	21,8	12,7	21,5	13,3	21,8	13,0	14,5	15,8	14,1
I
M	15,2	17,2	16,3	17,9	13,5	16,6	15,1	17,0	15,0

Требуется построить статистический ряд, гистограмму и эмпирическую функцию распределения для случайной величины m.

Решение.

Число интервалов, на которые разбивается диапазон наблюдений, равно

Принимая диапазон изменения ежесуточного выпуска поковок от 0 до 35 т/сут, получим ширину интервала

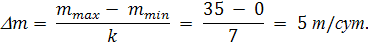
Тогда результаты наблюдений можно свести в представленный ниже статистический ряд. Значение m_i = 25 т/сут находится на границе 3-го и 4-го интервалов; его условно считаем принадлежащим в равной мере обоим интервалом, и поэтому к числу наблюдений прибавлено по 0,5.

Номер интервала i
Интервал, D m, т/сут	0…5	5…10	10…15	15…20	20…25	25…30	30…35
Среднее , т/сут	2,5	7,5	12,5	17,5	22,5	27,5	32,5
Число наблюдений ni			7,5	8,5
Частота, ni/n	0,0833	0,1666	0,2084	0,2362	0,1944	0,0833	0,0278

Построение гистограммы: по оси абсцисс откладываются интервалы и на каждом из них, как на основании, строится прямоугольник, площадь которого равна частоте данного интервала (с тем, чтобы площадь всей гистограммы была равна 1). В нашем случае все интервалы имеют одинаковую ширину и поэтому высоты прямоугольников равны соответствующим частотам (рис. 1.8).

Для построения эмпирической функции распределения достаточно нескольких точек, в качестве которых удобно взять границы интервалов:

F (0) = 0;

F (5) = F (0) + n₁/n = 0 + 0,0833 = 0,0833;

F (10) = F (5) + n₂/n = 0,0833 + 0,1666 = 0,2499;

F (15) = F (10) + n₃/n = 0,2499 + 0,2084 = 0,4583;

F (20) = F (15) + n₄/n = 0,4583 + 0,2362 = 0,6945;

F (25) = F (20) + n₅/n = 0,6945 + 0,1944 = 0,8889;

F (30) = F (25) + n₆/n = 0,8889 + 0,0833 = 0,9722;

F (35) = F (30) + n₇/n = 0,9722 + 0,0278 = 1.

График эмпирической функции распределения приведен на рис. 1.9.

Рисунок 1.8 – Гистограмма ежесуточного выпуска поковок.

Рисунок 1.9 – Эмпирическая функция распределения ежесуточного выпуска поковок; штриховой линией показана кривая для нормального закона распределения

 

Важнейшими характеристиками эмпирического распределения являются среднее арифметическое значение (выборочное среднее) и среднее квадратичное отклонение (выборочная дисперсия)

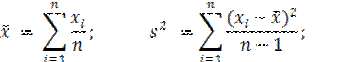
Уменьшение знаменателя в формуле для s ²на единицу объясняется тем, что в неё входит , значение которой зависит от наблюдаемых значений случайной величины Х. Другими словами, при вычислении среднего квадратичного отклонения на выборку наложена связь. Величина, зависящая от элементов выборки и входящая в формулу для вычисления какого-либо параметра, называется связью. Поэтому знаменатель такой формулы равен разности между объемом выборки n и числом связей l, наложенных на эту выборку. Эта разность f = (n - l) называется числом степеней свободы.

В отличие от соответствующих параметров теоретического распределения (математического ожидания M[X] и дисперсии D[X]) характеристики эмпирического распределения являются случайными величинами. Поэтому, произведя две серии наблюдений над случайной величиной Х, получим различные значения и s ². Однако при увеличении числа наблюдений n среднее арифметическое значение будет приближаться к математическому ожиданию. а среднее квадратичное отклонение – к дисперсии, т.е. при n→¥ справедливы соотношения → M[X] и s ²→ D[X].

Пример 1.8. Вычислить оценки математического ожидания, дисперсии и среднеквадратичного отклонения случайной величины, рассмотренной в предыдущем примере.

Решение.

Для статистического ряда, приведенного в примере 1.7, находим