Библиографический список. 1. Болотин В.В. Прогнозирование ресурса машин и конструкций

 

1. Болотин В.В. Прогнозирование ресурса машин и конструкций. - М.: Машиностроение, 1984. - 312 с.

2. Болотин В.В. Ресурс машин и конструкций. - М.: Машиностроение, 1990. – 448 с.

3. Ветошин А.Г., Марунин В.И. Надежность и безопасность технических систем. – Пенза: Изд-во Пензенского госуниверситета, 2002. – 129 с.

4. Гаркунов Д.Н. Триботехника. – М.: Машиностроение, 1985. – 424 с.

5. Гаркунов Д.Н. Триботехника: Учебник. – М.: Машиностроение, 1989. – 328 с.

6. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности, основные характеристики и их статистический анализ. – М.: Наука. – 1965. – 378 с.

7. ГОСТ 15467-79 (СТ СЭВ 3519-81). Управление качеством продукции. Основные понятия. Термины и определения.

8. ГОСТ 18322-78 (СТ СЭВ 5151-85). Система технического обслуживания и ремонта. Термины и определения.

9. ГОСТ 27.002-89: Надежность в технике. Основные понятия. Термины и определения.

10. ГОСТ 27.410-87. Надежность в технике. Методы контроля показателей надежности и планы контрольных испытаний на надежность.

11. Гребеник В.М., Гордиенко А.В., Цапко В.К. Повышение надежности металлургического оборудования: Справочник. – М.: Металлургия, 1988. – 688 с.

12. Гребеник В.М., Цапко В.К. Надежность металлургического оборудования (оценка эксплуатационной надежности): Справочник. – М.: Металлургия, 1980. – 344 с.

13. Жиркин Ю.В. Надежность, эксплуатация и ремонт металлургических машин: Учебник. – Магнитогорск, МГТУ, 2002. – 330 с.

14. Жиркин Ю.В. Надежность, эксплуатация, техническое обслуживание и ремонт металлургических машин. Руководство к решению задач и упражнений: Учебное пособие. – Магнитогорск, МГТУ, 1998. – 336 с.

15. Костецкий Б.И. Трение, смазка и износ в машинах. - Киев: Техника, 1970. – 346 с.

16. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. – М.: Машиностроение, 1977. – 526 с.

17. Надежность и долговечность машин / Б.И. Костецкий, И.Г. Носовский, Л.И. Бершадский и др. - Киев: Техника, 1975. –

18. Надежность технических систем: Справочник / Ю.К.Беляев, В.А.Богатырев, В.В.Болотин и др.; под ред. И.А.Ушакова. – М.: Радио и связь, 1985. – 608 с.

19. Орлов П.И. Основы конструирования: Справочно-методическое пособие в 3-х книгах. – М.: Машиностроение, 1977. - Кн. 1, 623 с.; Кн. 2, 574 с.; Кн. 3, 360 с.

20. Проников А.С. Надежность машин: Учебник. – М.: Машиностроение, 1978. – 542 с.

21. Проников А.С. Параметрическая надежность машин. – М.: МГТУ им. Н.Э.Баумана, 2003. – 560 с.

22. Решетов Д.Н. Работоспособность и надежность машин: Учебное пособие. – М.: Высшая школа, 1974. – 206 с.

23. Решетов Д.Н., Иванов С.А., Фадеев В.З. Надежность машин. – М.: Высшая школа,1988. – 120 с.

24. Трение, изнашивание и смазка: Справочник. В 2-х книгах / Под ред. И.В. Крагельского, В.В. Алисина. - М.: Машиностроение, 1982. – 400 с.

 

 

ПРИЛОЖЕНИЯ

 

Приложение А

 

Элементы теории вероятности и математической статистики, используемые в теории надежности

 

 

Вероятность события

 

Теория вероятностей изучает закономерности часто повторяющихся случайных явлений. Случайное явление - это такое явление, которое при неоднократном воспроизведении одного и того же опыта протекает каждый раз несколько по-иному.

Под событием в теории вероятностей понимают всякий факт, который в результате опыта может произойти или не произойти. Событие, которое в результате данного опыта может произойти, а может и не произойти, называется случайным. Событие называется достоверным, если оно в данном опыте неизбежно происходит, и невозможным, если оно в данном опыте заведомо произойти не может.

Примеры событий: поломка распорной плиты щековой дробилки за время t – случайное событие; отсутствие давления в трубопроводе при его разрыве – достоверное событие; наличие тока в электрической цепи при её разрыве – невозможное событие.

Вероятностью случайного события называется число, которое характеризует возможность появления события и принимает значения в диапазоне от 0 до 1. Вероятность события А обозначается Р(А), при этом Р(А)= 1, если А – достоверное событие, и Р(А)=0, если А – невозможное событие. Поэтому

0 £ Р(А) £ 1

Чтобы выявить на опыте закономерности случайных явлений, необходимо многократное проведение опыта при одних и тех же условиях. Пусть проведена серия из n опытов, в каждом из которых могло произойти или не произойти событие А. Частотой появления события А в данной серии опытов называется отношение числа опытов n _A , в которых появилось событие А, к общему числу опытов n. Частоту события часто называют статистической вероятностью. Отношение n _A/ n меняется в зависимости от числа проведенных опытов случайным образом. Однако при большом числе опытов частота события имеет тенденцию стабилизироваться, приближаясь к некоторому постоянному значению, вокруг которого происходят колебания с амплитудой, тем меньшей, чем больше общее число опытов. Таким образом

(1.1)

Тот факт, что с увеличением числа опытов эмпирические характеристики (частота события) приближаются к некоторым объективным характеристикам (вероятность события) данного случайного события, являются следствием весьма общего принципа, носящего название закона больших чисел.

Совокупность нескольких событий называется группой событий. Полная группа событий – совокупность событий, в которой хотя бы одно событие обязательно произойдет. Например, событие А (отказ изделия) и противоположное событие (безотказность изделия) составляют полную группу событий, так как изделие не может одновременно находиться в неисправном и исправном состоянии. События называются несовместными, если они не могут одновременно произойти в одном опыте; в противном случае они называются совместными.

Независимые события характеризуются тем, что появление одного из них не связано с появлением другого. Событие А считается независимым от события В, если вероятность события Р(А) не зависит от того, произошло событие В или нет. Например, выход из строя футеровки барабанной мельницы и её рабочее состояние являются несовместными и зависимыми событиями, которые образуют полную группу событий.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Рассмотрим два несовместных события А и В. Если при повторении опыта n раз события появлялись n _A и n _Враз, то частота события (А+В), состоящего в появлении или события А или события В, будет

(n _A + n _В)/ n = (n _A/ n) +(n _В/ n)

Если события А и В являются совместными, то при повторении опыта n раз возможно совместное появление этих событий с частотой n _AВ. Тогда

(n _A + n _В - n _AВ)/ n = (n _A/ n) +(n _В/ n) - (n _AВ/ n)

Заменяя частоты событий на соответствующие вероятности, придем к теореме сложения вероятностей

· для несовместных событий

Р(А+В) = Р(А) + Р(В) (1.2)

· для совместных событий

Р(А+В) = Р(А) + Р(В) – Р(АВ) (1.3)

где Р(АВ) – вероятность совместного появления событий А и В.

Полученные формулы можно обобщить для любого числа событий:

· для несовместных событий

· для совместных событий

Произведением нескольких событий называется событие, состоящее в одновременном появлении этих событий. Рассмотрим два события А и В, при чем событие А реализуется только в том случае, если произошло событие В. Тогда число совместных появлений событий равно числу появлений события А, т.е. n _AВ = n _А. Следовательно, выражение для частот событий имеет вид

n _AВ/ n = n _A/ n = (n _В/ n)´ (n _A/ n _В)

Заменяя частоты событий на соответствующие вероятности, придем к теореме умножения вероятностей

Р(АВ) = Р(В)´Р(А|В) (1.6)

Здесь Р(АВ) - вероятность одновременного появления событий А и В;

Р(А|В) - вероятность появления события А при условии, что произойдет событие В (условная вероятность).

Поскольку при применении теоремы умножения безразлично, какое из событий считать первым, а какое вторым, то

Р(АВ) = Р(А)´Р(В|А)

Вероятность произведения нескольких событий равна

Р(А₁А₂...А_m) = Р(А₁)´ Р(A₂|А₁))´Р(A₃|А₁A₂))´…´Р(A_m|А₁A₂…A_m-1)

В случае независимых событий теорема умножения упрощается к виду

где P - знак произведения.

Пример 1.1. Вероятность безотказной работы привода барабанной мельницы (событие А) зависит от 4-х соединенных последовательно узлов: электродвигателя (А₁), муфты (А₂), редуктора (А₃), открытой зубчатой передачи (А₄). Вероятность безотказной работы: первого узла - Р(А₁) = 0,95; второго - Р(А₂) = 0,85; третьего - Р(А₃) = 0,90; четвертого - Р(А₄) = 0,80. Найти вероятность безотказной работы привода, если каждый из 4-х узлов может выйти из строя независимо от трех других.

Решение.

По теореме умножения для независимых событий (1.7) находим

Р(А) = Р(А₁)´ Р(A₂´Р(A₃)´Р(A₄) = 0,95´0,85´0,90´0,80 = 0,58.

Пример 1.2. В системе централизованной циркуляционной системы жидкой смазки используется два параллельно работающих фильтра. Примем, что вероятность безотказной работы первого фильтра – Р(А) = 0,9, а второго фильтра – Р(В) = 0,9. Найти вероятность отсутствия одновременного отказа обоих фильтров при условии независимости отказов фильтров.

Решение.

Безотказная работа одного из фильтров или обоих вместе есть сумма событий (А+В). Вероятность отсутствия одновременного отказа обоих фильтров при условии независимости отказов определяется по формуле (1.3)

Р(А+В) = Р(А) + Р(В) – Р(АВ) = 0,9 + 0,9 – 0,9 ´0,9 = 0,99.

 

Случайные величины

 

Случайной величиной называется величина, которая в результате опыта может принять одно из возможных значений, заранее неизвестное и зависящее от случайных причин. Случайным величинам противопоставляются детерминированные величины, значения которых предопределяются начальными условиями.

Для характеристики случайной величины, прежде всего, необходимо задать набор её допустимых значений. Различают дискретные и непрерывные случайные величины. Дискретной называется случайная величина, которая может принимать конечное или бесконечное счетное множество значений. Другими словами, возможные значения дискретной случайной величины можно заранее перечислить. Непрерывной называется случайная величина, которая может принимать все значения из некоторого конченого или бесконечного промежутка числовой оси. Поэтому значения непрерывной случайной величины не могут быть заранее перечислены – они непрерывно заполняют некоторый промежуток.

Примеры.

1) Число выплавленных металлических заготовок – случайная дискретная величина; масса выплавленного металла – непрерывная случайная величина.

2) Число футеровочных плит щековой дробилки, замененных в процессе ремонтного цикла - случайная дискретная величина; время безотказной работы футеровочной плиты - случайная непрерывная величина.

Условимся случайные величины обозначать большими буквами, а их возможные значения – малыми буквами.

Пусть дана дискретная случайная величина Х с возможными значениями х ₁, х ₂, …, х _n, каждое из которых может появиться в результате опыта с вероятностью соответственно p ₁, p ₂, …, p _n. Сумма вероятностей всех возможных значений дискретной случайно величины равна единице, т.е.

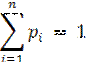
Эта формула отражает тот факт, что событие (случайная величина принимает в результате опыта одно из своих возможных значений) является достоверным.

Случайная величина считается полностью описанной с вероятностной точки зрения, если задан закон её распределения. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон можно задать таблично (ряд распределения), графически (многоугольник или гистограмма распределения) и аналитически (в виде формулы или уравнения).

Пример 1.3. Допустим, что каким-либо путем установлена вероятность разрушения распорной плиты щековой дробилки в течение 1-го месяца её эксплуатации и она оказалась равной р = 0,2. Обозначив число месяцев работы через Х, найти закон распределения случайной величины Х.

Решение.

Возможные значения величины Х равны 1, 2, 3,…(теоретически они ничем не ограничены). Для удобства расчетов введем вероятность неразрушения матрицы, т.е. величину q = 1 – р = 1 – 0,2 = 0,8.

Величина Х = 1, если плита разрушилась в 1-й месяц эксплуатации. Вероятность такого события равна р ₁ = p = 0,2.

Для того чтобы величина Х приняла значение 2, необходимо, чтобы в 1-й месяц эксплуатации плита не разрушилась, а во 2-м разрушилась. Вероятность такого события равна р ₂ = р×q = 0,2×0,8 = 0,16.

Вероятность того, что разрушение матрицы произойдет в течение n- го месяца, будет равна

.

Это соответствует аналитической форме задания закона распределения случайной величины

Ряд распределения величины Х имеет следующий вид (табличная форма задания закона распределения):

х₁ = 1, р ₁ = p = 0,2;

х₂ = 2, р ₂ = р₁×q = р×q = 0,2×0.8 = 0,16;

х₃ = 3, р ₃ = р₂×q = р×q² = 0,2×0.8² = 0,128 и т.д.

Графическая форма задания закона распределения дана на рис. 1.4.

Более универсальной характеристикой случайной величины является функция распределения F(x), под которой понимают вероятность обнаружить значение X < x, где x – некоторая текущая переменная, т.е.

По определению функция распределения является неубывающей функцией своего аргумента x, т.е. F(x ₂ ) > F(x ₁ ) при x ₂ > x ₁. При этом F (-¥)= 0 и F (+¥) = 1.

Рисунок 1.4. – Графическая форма задания закона распределения в виде многоугольника (верх) и гистограммы (низ) распределения вероятности разрушения плиты в зависимости от числа месяцев работы.

В теории надежности функцию распределения F(x) называют также вероятностью отказа элемента до момента t.

В отличие от ряда и многоугольника функция F(x) существует как для дискретных, так и для непрерывных случайных величин (рис. 1.5).

 

 

Рисунок 1.5. – Функция распределения для дискретной (а) и непрерывной (б) случайной величины Х.

 

Если случайная величина Х может принимать дискретные значения, то распределение называется дискретным. В этом случае функция распределения является ступенчатой, скачки которой происходят в точках, соответствующих возможным значениям случайной дискретной величины Х, и равны вероятности этих значений. Очевидно, сумма всех скачков равна 1.

Пример 1.4. Построить эмпирическую функцию распределения случайной величины Х по данным примера 1.3.

Решение.

Вероятность разрушения распорной плиты щековой дробилки в течение 1-го месяца её эксплуатации равна р = 0,2. Вероятность разрушения плиты в течение 2-го месяца равна р×q = 0,2×0.8 = 0,16, и поэтому вероятность разрушения в течение первых двух месяцев будет (р + р×q). Следовательно, вероятность P_n(A) того, что в течение первых n месяцев событие А (разрушение плиты) произойдет хотя бы один раз, будет

График функции распределения для случая р = 0,2 и q = 0,8 представлен на рис. 1.6.

Рисунок 1.6 – Эмпирическая функция распределения числа месяцев работы распорной плиты щековой дробилки

 

Если случайная величина имеет непрерывное распределение, то функция распределения F(x) является непрерывной и дифференцируемой. Первая производная от функции распределения называется плотностью распределения случайной величины Х

График плотности распределения случайной величины называется кривой распределения. Плотность распределения полностью определяет случайную величину и является неотрицательной функцией, т.е. f(x) ³ 0.

Функция F(x), как любая вероятность, есть величина безразмерная. Размерность плотности распределения f(x) обратна размерности случайной величины.

Вероятность того, что значения случайной величины Х будет лежать в интервале между х₁ и х₂, равна

Вероятность обнаружить величину Х во всем интервале -¥ ≤ Х ≤ +¥, очевидно равна 1, так как это достоверное событие, и поэтому площадь под кривой распределения равна 1, т.е.

При решении задач надежности часто нет необходимости характеризовать случайную величину плотностью распределения, а достаточно указать только числовые характеристики, отражающие наиболее существенные особенности распределения случайной величины. Такие параметры называются числовыми характеристиками случайной величины.

В качестве характеристики положения случайной величины, указывающей некоторое среднее значение, вокруг которого группируются её значения, обычно применяют математическое ожидание.

Пусть в результате n опытов найдено, что случайная величина Х принимает n ₁ раз значение х ₁, n ₂ раз значение х ₂ и т.д. Тогда среднее арифметическое значение случайной величины Х будет равно

Здесь m – число групп с одинаковым значением случайной величины x_i.

Если – заменить эмпирические частоты (n _i/ n) вероятностями P_i, то среднему арифметическому значению случайной величины Х будет соответствовать теоретическая характеристика случайной величины

 

Эта величина называется математическим ожиданием (средним значением) случайной величины Х.

Для непрерывного распределения случайной величины

Характеристикой рассеивания (разброса) значений случайной величины около её математического ожидания является дисперсия D_x, под которой понимают математическое ожидание квадрата отклонения случайной величины от её математического ожидания.

Для дискретной случайной величины

Для непрерывной случайной величины

Оценка дисперсии случайной величины D_х*:

Так как дисперсия имеет размерность квадрата измеряемой величины, то для удобства практического использования вводят среднеквадратичное отклонение (или стандарт), размерность которого совпадает с размерностью случайной величины

Для оценки рассеяния с помощью безразмерной величины используют коэффициент вариации, который равен:

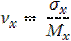
Математическое ожидание и дисперсия случайной величины являются её основными характеристиками. Кроме них, в теории надежности для характеристики положения случайной величины используют медиану и моду, а для характеристики формы – коэффициенты асимметрии и эксцесс.

Пример 1.5. Найти математическое ожидание и среднеквадратичное отклонение случайной величины Х по данным примера 1.3.

Решение.

Возможным значениям случайной величины Х, равным x_i = 1, 2, …, i, … ¥, соответствуют вероятности P_i = p, p×q, …, p×q^i--1, …, 0.

Математическое ожидание величины Х (число месяцев до разрушения распорной плиты) выражается суммой ряда

Дисперсия случайной величины Х будет равна

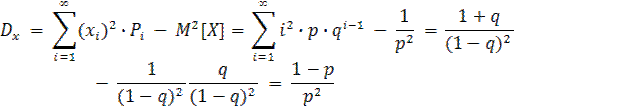
Следовательно, среднеквадратичное отклонение равно

При вероятности разрушения плиты в 1-й месяц эксплуатации p = 0,2, математическое ожидание срока службы составит M _x = 5 месяцев, дисперсия D _x = 20 мес², а среднеквадратичное отклонение σ_x = 4,5 месяца.