Рассмотрим первую краевую задачу для уравнения Пуассона в прямоугольной области 0 ≤ x ≤ α; 0 ≤ y ≤ b;
Uxx+Uyy=f (x,y), (12.7)
(ГУ) Ur=φ (x,y). (12.8)
Выбрав шаги по времени и по координатам, строим сетку
xl = l · h; x 0 = 0; xl = l · h; xn = α; yJ = J · τ; y 0 = 0; ym = b
где t = 1, 2 ,….,n; J = 1, 2 ,……., m.
Заменяя в каждом внутреннем узле (xl, yJ) производные конечными разностями по формулам (12.4), получаем конечно-разностные уравнения
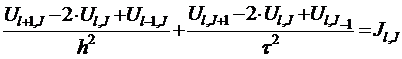 , (12.9)
, (12.9)
U 0, J = φ (0 ,yJ) = φ 0, J; Un,J = φ (α,yJ) = φn,J, (12.10)
Ul, 0 = φ (x, 0) = φl, 0; Ul,m= φ (x,b) = φl,m, (12.11)
где t = 1, 2 ,…., n; J = 1, 2 ,……., m.
Уравнения (12.9) вместе с условиями (12.10)-(12.11) образуют систему линейных алгебраических уравнений относительно Ul,J. Число неизвестных и число уравнений в системе равно числу внутренних узлов сетки. Схема узловых точек для уравнений (12.9) изображена на рис. 12.1.
Если h = τ и Jl,J = 0, то конечно-разностные уравнения имеют вид
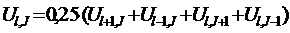 (12.12)
(12.12)
Пример 1. Найти решение уравнения теплопроводности
Uxx=Ut; 0 ≤ x ≤ 1; t ≥ 0;
(НУ) U (x, 0) =4 · x · (1 -x);
(ГУ) U (0 ,t) =U (1 ,t) = 0
методом сеток с точностью до ε = 0.001 на первых трех временных уровнях, если шаг по координате Δ x = h = 0,1, по времени Δ t = τ = 1/600.
Решение. Для вычисления Ul,J воспользуемся системой конечно-разностных уравнений (12.9) при g = 0:
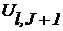 =
= 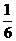 (
(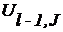 +
+ 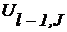 )+
)+ 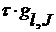 , (12.13)
, (12.13)
(НУ) Ul, 0 = 4 · xl · (1 -xl); l = 1, 2 ,…., 10, (12.14)
(ГУ) U 0, J= U 10, J = 0; J= 0,1,2. (12.15)
Составим таблицу значений Ul,J (табл. 12.1).
Таблица 12.1
| l J | |||||||||||
| 0.360 | 0.640 | 0.840 | 0.960 | 0.960 | 0.840 | 0.640 | 0.360 | ||||
| 0.347 | 0.627 | 0.827 | 0.977 | 0.987 | 0.977 | 0.827 | 0.627 | 0.347 | |||
| 0.336 | 0.613 | 0.813 | 0.933 | 0.973 | 0.933 | 0.813 | 0.613 | 0.336 |
В силу симметрии начальных и краевых условий относительно оси x = 0,5 решение Ul,J будет симметричным относительно этой же оси.
Это позволяет вести расчеты для t = 1, 2 ,…., 5, а для остальных значений следует заполнить таблицу, исходя из свойства симметрии:
U 0, J = U 10, J; U 1, J = U 9, J; U 2, J = U 8, J; U 3, J = U 7, J; U 4, J = U 6, J.
Начальная строка этой таблицы (J = 0) заполняется на основании зaданного начального условия (12.14).
В первый (l = 0) и последний (l = 10) столбцы вписываются данные граничных условий (12.15). Остальные строки таблицы последовательно заполняются с помощью применения расчетной формулы (12.13). На первом шаге
Ul,J = (1/6) · 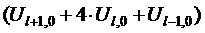 .
.
Например,
U 1,1 = (1/6) · 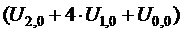 = (1/6) · (0,640+4∙0,360) = 0,347.
= (1/6) · (0,640+4∙0,360) = 0,347.
На втором шаге
Ul,2 = (1/6) · 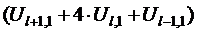 .
.
Пример 2. Применяя метод сеток с шагом h = τ = 1/3, найти решениеуравнения Лапласа в квадрате с вершинами А (0,0), В (0,1), С (1,1), D (1,0), удовлетворяющее краевым условиям
U (0 ,y) = 30 · y; U (x, 1) = 30 · (1 -x 2); U (1 ,y) = 0; U (x, 0) = 0.
Решение. Конечно-разностные уравнения для уравнения Лапласа при h = τ = 1/3имеют вид:
U0,J = 0,25 · 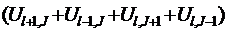 , (12.16)
, (12.16)
(ГУ) U0,J = 30 · J · h; U 3, J = 0; (12.17)
(НУ) (Ul, 0 = 0; Ul, 3 = 30 · (1 - (l · h)2), (12.18)
где x = l · h, y = J · h, l = 1,2,3, J = 0,1,2,3.
Составим таблицу Ul,J (табл. 12.2)
Таблица 12.2
| y x | 1/3 | 2/3 | ||
| U 0,0 = 0 | U0 ,1 = 10 | U 0,2 = 20 | U 0,3 = 30 | |
| 1/3 | U l,0 = 0 | U l,1 | U l,2 | U l,3 = 26,67 |
| 2/3 | U 2,0 = 0 | U 2,1 | U 2,2 | U 2,3 = 16,67 |
| U 3,0 = 0 | U 3,1 = 0 | U 3,2 = 0 | U 3,3 = 0 |
Первая и последняя строки этой таблицы получены из граничных условий (12.17), а первый и последний столбцы - из (12.18).
U l,1, U l,2, U 2,1, U 2,2 находимиз следующей системы линейных алгебраических уравнений, которые получены из расчетной формул (12.16):
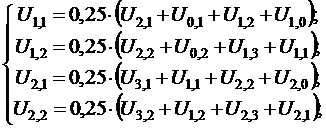
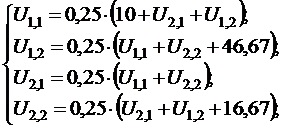
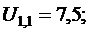
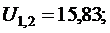
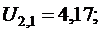
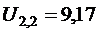 .
.
 2017-12-14
2017-12-14 1484
1484
